Calculus war ursprünglich als Infinitesimalrechnung oder „Kalkül der Infinitesimalzahlen“ bekannt. Die Infinitesimalsrechnung entstand im 17. Jahrhundert.
Es wird so genannt, weil es so ist, als würde man kleine Kieselsteine verwenden, um etwas zu berechnen. Die Differenzierung im Kalkül schneidet etwas in kleine Stücke, um über seine Änderungen Bescheid zu wissen. Die Integration in Calculus fügt die kleinen Teile zusammen, um die Mengen zu kennen.
Infinitesimalrechnung ist die Lehre vom kontinuierlichen Wandel.
Die beiden Dur Zweige, die in der Analysis verwendet werden, sind Differenzierung und Integration. Viele Studenten und sogar Gelehrte sind nicht in der Lage, den Unterschied zu verstehen.
Key Take Away
- Differenzierung ist eine mathematische Operation in der Analysis, die die Änderungsrate oder Steigung einer Funktion an einem bestimmten Punkt berechnet.
- Integration ist die Umkehroperation der Differentiation, bei der die akkumulierte Summe der Werte einer Funktion über ein bestimmtes Intervall berechnet wird, um Flächen, Volumina oder andere Größen zu ermitteln.
- Sowohl Differenzierung als auch Integration sind wesentliche Konzepte in der Analysis, aber sie dienen entgegengesetzten Zwecken, wobei sich die Differenzierung auf Änderungsraten und die Integration auf Akkumulation konzentriert.
Differenzierung vs. Integration
Der Unterschied zwischen Differenzierung und Integration besteht darin, dass die Differenzierung verwendet wird, um die sofortigen Änderungsraten und die Steigungen von Kurven zu finden. Wenn du müssen Berechnen Sie die Fläche unter Kurven, verwenden Sie Integration. Wie Sie sehen können, sind Differenzierung und Integration in mathematischer Bedeutung entgegengesetzt.
Vergleichstabelle
| Vergleichsparameter | Differenzierung | Integration |
|---|---|---|
| Zweck | Die Differenzierung wird verwendet, um die Steigung einer Kurve zu berechnen. Es wird verwendet, um die sofortigen Änderungsraten von einem Punkt zum anderen herauszufinden. | Die Integration wird verwendet, um die Fläche unter oder zwischen den Kurven zu berechnen. |
| Anwendung aus dem wirklichen Leben | Die Differentiation wird verwendet, um die Momentangeschwindigkeit zu berechnen. Es wird auch verwendet, um herauszufinden, ob eine Funktion zunimmt oder abnimmt. | Die Integration wird verwendet, um die Fläche gekrümmter Oberflächen zu berechnen. Es wird auch verwendet, um das Volumen von Objekten zu berechnen. |
| Addition und Division | Die Differenzierung verwendet die Division, um die momentane Geschwindigkeit oder beliebige gewünschte Ergebnisse zu berechnen. | Die Integration verwendet Addition für ihre Berechnungen. |
| DIREKT VOR | Differenzierung ist der umgekehrte Prozess der Integration. | Integration ist der umgekehrte Prozess der Differenzierung. |
| Rollen | Die Differenzierung wird verwendet, um die Geschwindigkeit der Funktion zu berechnen, da sie die Momentangeschwindigkeit berechnet. | Die Integration wird verwendet, um die von einer beliebigen Funktion zurückgelegte Strecke zu berechnen, da sie die Fläche unter der Kurve berechnet. |
Was ist Differenzierung?
In der Mathematik die Methode zum Ermitteln der Änderungsrate einer Funktion oder zum Ermitteln der Derivat wird als Differenzierung bezeichnet.
Die drei Ableitungen sind:
- Algebraische Funktionen- D(xn) = nxn - 1
- Trigonometrische Funktionen- D(ohne x) = cos x
- Exponentialfunktionen- D(ex) = ex
Die Differenzierung wird verwendet, um die Steigung einer Kurve zu berechnen und die momentanen Änderungsraten von einem Punkt zum anderen herauszufinden.
Es gibt eine „Kettenregel“, die hilft, zusammengesetzte Funktionen zu unterscheiden. Die Berechnung der Momentangeschwindigkeit ist eine der Echtzeitverwendungen der Differentiation.
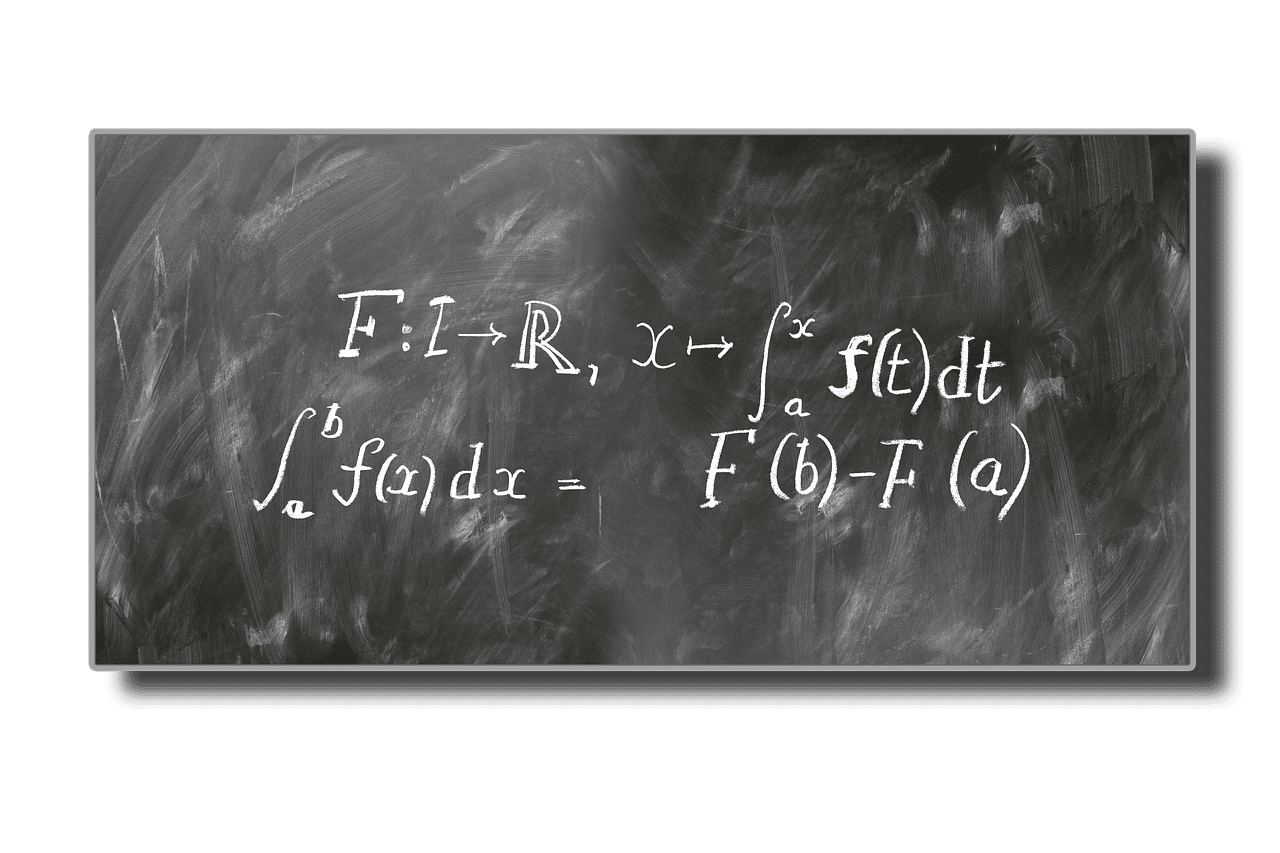
Was ist Integration?
In der Analysis bezieht sich die Integration auf die Formel und die Methode, mit der die Fläche unter der Kurve berechnet wird. Es wird zur Berechnung verwendet, da es sich nicht um eine perfekte Form handelt, für die die Website berechnet werden kann.
Die Integration wird verwendet, um die Entfernung zu ermitteln, die von einer beliebigen Funktion zurückgelegt wird. Der von der Funktion zurückgelegte Weg ist die Fläche unter der Kurve.
Letzte Aktualisierung: 11. Juni 2023
Ich habe mir so viel Mühe gegeben, diesen Blogbeitrag zu schreiben, um Ihnen einen Mehrwert zu bieten. Es wird sehr hilfreich für mich sein, wenn Sie es in den sozialen Medien oder mit Ihren Freunden / Ihrer Familie teilen möchten. TEILEN IST ♥️
Emma Smith hat einen MA-Abschluss in Englisch vom Irvine Valley College. Sie ist seit 2002 Journalistin und schreibt Artikel über die englische Sprache, Sport und Recht. Lesen Sie mehr über mich auf ihr Bio-Seite.
Die praktischen Auswirkungen der Integration und ihre Rolle bei der Berechnung realer Werte werden effektiv erklärt. Es schließt die Lücke zwischen Theorie und Anwendung.
Tatsächlich kann das Verständnis der Rolle der Integration in praktischen Szenarien die Wertschätzung für ihre Bedeutung steigern.
Dies ist ein Artikel für Anfänger, die die Grundlagen der Analysis verstehen möchten. Die Erklärung von Differenzierung und Integration ist gut formuliert.
Ich stimme zu, der Artikel dient als nützliche Ressource für diejenigen, die eine solide Grundlage in der Analysis aufbauen möchten.
Die Unterscheidung zwischen algebraischen, trigonometrischen und exponentiellen Funktionen in der Differentiation wird gut erläutert und trägt zu einem tieferen Verständnis von Ableitungen bei.
Auf jeden Fall bietet die Aufschlüsselung der Derivattypen einen umfassenden Überblick über die Differenzierung.
Der Abschnitt „Was ist Differenzierung?“ vermittelt ein klares Verständnis des Zwecks und der Verwendung der Differenzierung und erleichtert so das Verständnis für den Einzelnen.
Die Hervorhebung des Echtzeiteinsatzes der Differenzierung bietet auf jeden Fall einen wertvollen Kontext für ihre Anwendung.
Die Erklärung der „Kettenregel“ war besonders aufschlussreich. Es verleiht der Diskussion über Differenzierung Tiefe.
Der historische Kontext zur Infinitesimalrechnung ist aufschlussreich. Es ist von entscheidender Bedeutung, die Ursprünge einer solch zentralen mathematischen Disziplin zu verstehen.
Ich fand die Erklärung zu Differenzierung vs. Integration sehr klar und informativ. Es hat mir geholfen, das Konzept besser zu verstehen.
Auf jeden Fall kann die Aufschlüsselung ihrer Unterschiede dabei helfen, das eigene Verständnis der Infinitesimalrechnung zu festigen.
Der Artikel bietet einen umfassenden Überblick über Differenzierung und Integration. Der Schwerpunkt auf realen Anwendungen macht es ansprechender.
Ich kann nur zustimmen. Die Verknüpfung von Analysis mit Beispielen aus der Praxis hilft dabei, das Interesse der Lernenden zu wecken.
Das Konzept der Differenzierung und Integration kann in verschiedenen realen Anwendungen gesehen werden. Wenn Sie dies verstehen, können Sie in vielen Bereichen wertvolle Erkenntnisse gewinnen.
Die Anwendbarkeit der Infinitesimalrechnung geht auf jeden Fall über den akademischen Bereich hinaus und kann in praktischen Szenarien von Vorteil sein.
Tatsächlich kann das Verständnis von Analysis-Konzepten zahlreiche Möglichkeiten in verschiedenen Branchen eröffnen.
Die Erklärung der Integration als Methode zur Berechnung der Fläche unter der Kurve ist auf eine Weise formuliert, die dieses komplexe Konzept vereinfacht.
Einverstanden ist, dass die Klarheit der Erklärung die Integration einem breiten Publikum zugänglicher macht.
Die bereitgestellte Vergleichstabelle ist eine praktische Referenz zum Verständnis der Nuancen von Differenzierung und Integration. Es vereinfacht komplexe Konzepte.