Le calcul était initialement connu sous le nom de calcul infinitésimal ou "le calcul des infinitésimaux". Le calcul des infinitésimaux est né au 17ème siècle.
On l'appelle ainsi parce que c'est comme utiliser de petits cailloux pour calculer quelque chose. La différenciation en calcul divise quelque chose en petits morceaux pour connaître ses changements. L'intégration dans Calculus joint les petits morceaux ensemble pour connaître les quantités.
Calcul est l'étude du changement continu.
Les deux majeur les branches utilisées dans le calcul sont la différenciation et l'intégration. Merci beaucoup les étudiants et même les universitaires ne sont pas capables de comprendre sa différence.
Faits marquants
- La différenciation est une opération mathématique de calcul qui calcule le taux de variation ou la pente d'une fonction à un point spécifique.
- L'intégration est l'opération inverse de différenciation, calculant la somme accumulée des valeurs d'une fonction sur un intervalle donné, utilisée pour trouver des surfaces, des volumes ou d'autres quantités.
- La différenciation et l'intégration sont des concepts essentiels en calcul, mais ils servent des objectifs opposés, la différenciation se concentrant sur les taux de changement et l'intégration sur l'accumulation.
Différenciation vs Intégration
La différence entre la différenciation et l'intégration est que la différenciation est utilisée pour trouver les taux de changement instantanés et les pentes des courbes. Si tu doivent calculez l'aire sous les courbes, utilisez l'intégration. Comme vous pouvez le voir, la différenciation et l'intégration sont opposées en termes mathématiques.
Tableau de comparaison
| Paramètres de comparaison | Différenciation | Intégration |
|---|---|---|
| Objectif | La différenciation est utilisée pour calculer la pente d'une courbe. Il est utilisé pour connaître les taux de variation instantanés d'un point à un autre. | L'intégration est utilisée pour calculer l'aire sous ou entre les courbes. |
| Application réelle | La différenciation est utilisée pour calculer la vitesse instantanée. Il est également utilisé pour déterminer si une fonction est croissante ou décroissante. | L'intégration est utilisée pour calculer l'aire des surfaces courbes. Il est également utilisé pour calculer le volume des objets. |
| Addition et division | La différenciation utilise la division pour calculer la vitesse instantanée ou tout résultat souhaité. | L'intégration utilise l'addition pour ses calculs. |
| JUSTE EN FACE DU | La différenciation est le processus inverse de l'intégration. | L'intégration est le processus inverse de différenciation. |
| Rôle | La différenciation est utilisée pour calculer la vitesse de la fonction car elle calcule la vitesse instantanée. | L'intégration est utilisée pour calculer la distance parcourue par n'importe quelle fonction car elle calcule l'aire sous la courbe. |
Qu'est-ce que la différenciation ?
En mathématiques, la méthode pour trouver le taux de variation d'une fonction ou trouver la dérivé est connue sous le nom de différenciation.
Les trois dérivés sont :
- Fonctions algébriques- D(xn) = nxn - 1
- Fonctions trigonométriques- D(sans pour autant x) = cos x
- Fonctions exponentielles- D(ex) = ex
La différenciation est utilisée pour calculer la pente d'une courbe et pour connaître les taux de variation instantanés d'un point à un autre.
Il existe une « règle de chaîne » qui aide à différencier les fonctions composites. Le calcul de la vitesse instantanée est l'une des utilisations en temps réel de la différenciation.
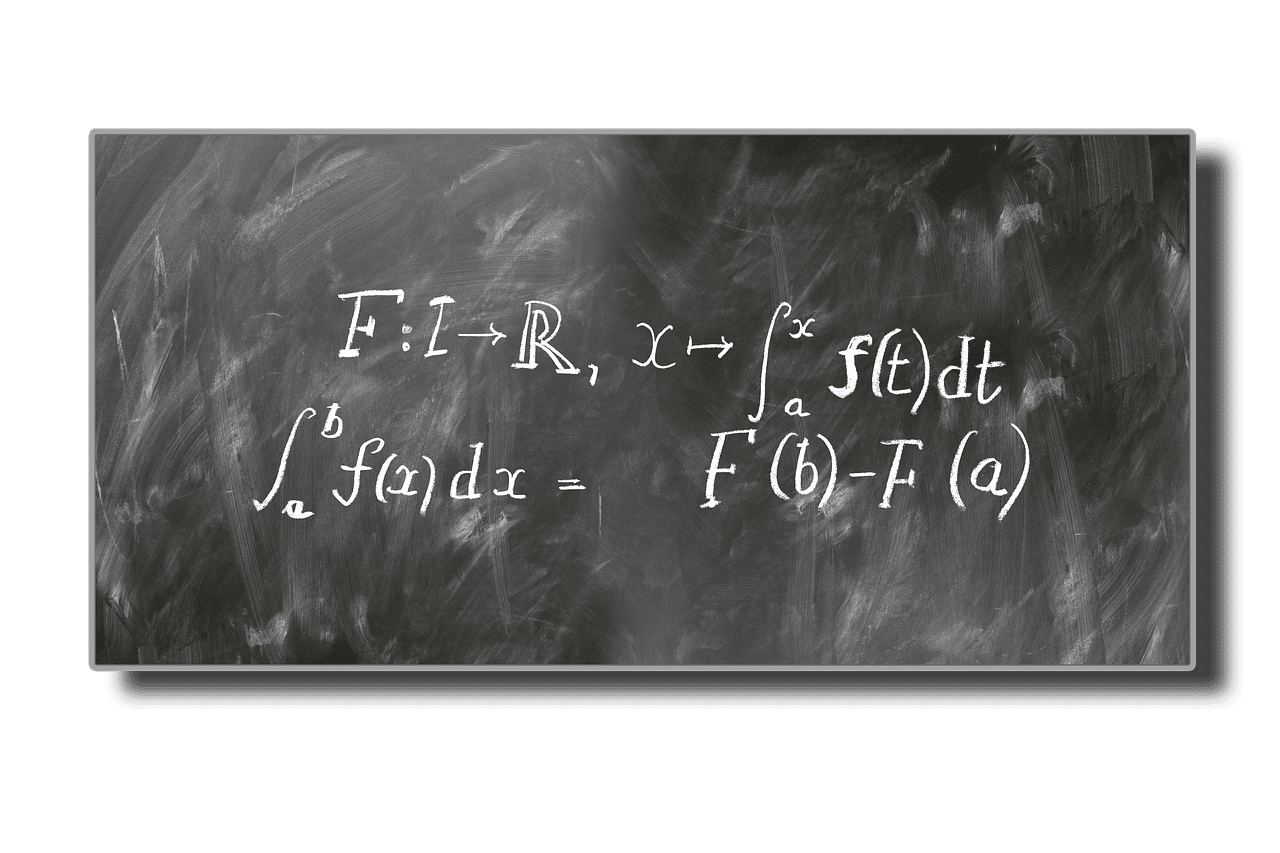
Qu'est-ce que l'intégration ?
En calcul, l'intégration fait référence à la formule et à la méthode utilisées pour calculer l'aire sous la courbe. Il est utilisé pour le calculer car il ne s'agit pas d'une forme parfaite pour laquelle le site peut être calculé.
L'intégration est utilisée pour trouver la distance parcourue par n'importe quelle fonction. La distance parcourue par la fonction est l'aire sous la courbe.
Dernière mise à jour : 11 juin 2023
J'ai mis tellement d'efforts à écrire ce billet de blog pour vous apporter de la valeur. Cela me sera très utile, si vous envisagez de le partager sur les réseaux sociaux ou avec vos amis/famille. LE PARTAGE C'EST ♥️
Emma Smith est titulaire d'une maîtrise en anglais du Irvine Valley College. Elle est journaliste depuis 2002, écrivant des articles sur la langue anglaise, le sport et le droit. En savoir plus sur moi sur elle page bio.
Les implications pratiques de l'intégration et son rôle dans le calcul des valeurs du monde réel sont expliquées efficacement. Il comble le fossé entre la théorie et l’application.
En effet, comprendre le rôle de l'intégration dans des scénarios pratiques peut améliorer l'appréciation de son importance.
Ceci est un article destiné aux débutants qui souhaitent comprendre les bases du calcul. L’explication de la différenciation et de l’intégration est bien articulée.
Je suis d'accord, l'article constitue une ressource utile pour ceux qui souhaitent construire une base solide en calcul.
La distinction entre les fonctions algébriques, trigonométriques et exponentielles dans la différenciation est bien élucidée, contribuant à une compréhension plus approfondie des dérivées.
Absolument, la répartition des types de dérivés fournit un aperçu complet de la différenciation.
La section « Qu'est-ce que la différenciation ? » donne une compréhension claire du but et de l’utilisation de la différenciation, ce qui la rend plus facile à comprendre pour les individus.
Assurément, mettre en évidence l’utilisation en temps réel de la différenciation fournit un contexte précieux pour son application.
L’explication de la « règle de la chaîne » était particulièrement perspicace. Cela ajoute de la profondeur à la discussion sur la différenciation.
Le contexte historique fourni sur le calcul est éclairant. Il est crucial de comprendre les origines d’une discipline mathématique aussi cruciale.
J'ai trouvé l'explication sur la différenciation vs l'intégration très claire et informative. Cela m'a aidé à mieux comprendre le concept.
Assurément, la décomposition de leurs différences peut aider à consolider la compréhension du calcul.
L'article présente un aperçu complet de la différenciation et de l'intégration. L'accent mis sur les applications réelles le rend plus attrayant.
Je ne pourrais pas être plus d'accord. Relier le calcul à des exemples concrets aide à capter l’intérêt des apprenants.
Le concept de différenciation et d'intégration peut être vu dans diverses applications réelles. Comprendre cela peut fournir des informations précieuses dans de nombreux domaines.
Absolument, l’applicabilité du calcul s’étend au-delà du domaine académique et peut être bénéfique dans des scénarios pratiques.
En effet, la compréhension des concepts de calcul peut ouvrir de nombreuses opportunités dans divers secteurs.
L'explication de l'intégration en tant que méthode de calcul de l'aire sous la courbe est articulée de manière à simplifier ce concept complexe.
D'accord, la clarté de l'explication rend l'intégration plus accessible à un large public.
Le tableau de comparaison fourni est une référence pratique pour comprendre les nuances de la différenciation et de l'intégration. Cela simplifie des concepts complexes.