T 検定と Z 検定: 違いと比較

t 検定は、母集団の標準偏差が不明な場合、またはサンプル サイズが小さい場合にサンプル平均を比較するために使用されます。一方、z 検定は、母集団の標準偏差が既知でサンプル サイズが十分に大きい場合に適しています。

主要な取り組み

1. T 検定は、母集団の標準偏差が不明な場合に XNUMX つのグループの平均を比較するために使用されます。Z 検定は、母集団の標準偏差が既知であり、サンプル サイズが大きい場合に使用されます。
2. t 検定は t 分布に依存します。t 分布は、サンプル サイズが小さく、母集団の標準偏差が不明な場合に使用されますが、Z 検定では標準正規分布が使用されます。
3. 実際には、既知の母集団標準偏差が希少であるため、t 検定がより一般的です。同時に、Z 検定はサンプル サイズが大きく、母集団パラメータが既知である状況のために予約されています。

T検定とZ検定

Z 検定は、母集団の平均と標準偏差がわかっている場合に使用され、母集団が正規分布していると仮定します。 t 検定は、母集団の標準偏差が不明な場合に使用され、 サンプル データ。 ザ・ t検定 サンプルが正規分布していると仮定します。

T 検定はサンプル サイズが限られている問題に最適ですが、Z 検定はサンプル サイズが大きい問題に最適です。

比較表

側面	T検定	Z検定
使用事例	サンプルサイズが小さい（<30）場合、または母集団の標準偏差が不明な場合に使用されます。	サンプルサイズが大きく (>30)、母集団の標準偏差がわかっている場合に使用されます。
サンプルサイズ	サンプルサイズが小さい場合に適しています。	大きなサンプルサイズに適しています。
式	t = (x̄ – μ) / (s / √n)	z = (x̄ – μ) / (σ / √n)
母集団パラメータ	通常、母集団パラメータ (平均と標準偏差) が不明な場合に使用されます。	通常、母集団パラメータ (平均および標準偏差) が既知または推定されている場合に使用されます。
自由度	1 サンプルの t 検定に n-XNUMX の自由度 (n はサンプル サイズ) を使用します。	XNUMX サンプルの Z 検定に n 自由度を使用します。
分散の仮定	標本分散が母集団分散の不偏推定量であると仮定します。	母集団の分散が既知であるか、サンプルから合理的に推定できることを前提としています。
販売	標準の正規 (z) 分布と比較して裾が重い t 分布に従います。	標準の正規 (z) 分布に従います。
例	サンプルサイズが小さく、母集団の標準偏差が不明な場合に、XNUMX つの異なるグループの平均テストスコアが大きく異なるかどうかを検定します。	サンプルサイズが大きく、母集団の標準偏差が既知である場合に、母集団の平均身長が既知の値と大きく異なるかどうかを検定します。
統計ソフト	通常、R、Python、統計計算機などのソフトウェアを使用して実行されます。	通常、R、Python、統計計算機などのソフトウェアを使用して実行されます。

T検定とは？

t 検定は、2 つのグループの平均を比較し、それらの間に有意な差があるかどうかを判断するために使用される統計手法です。データが正規分布に従う場合、仮説検定でよく使用されます。

T 検定の種類

1. 独立したサンプルの T 検定:
   • 2 つの独立したグループの平均を比較する場合に使用されます。
   • 仮定: 各グループのデータは正規分布しており、分散はほぼ等しい。
2. 対応のあるサンプルの T 検定:
   • 測定の前後など、関連する 2 つのグループの平均を比較する場合に適用されます。
   • 仮定: ペアになった観測間の差異は正規分布します。

T 検定における仮説

T 検定では、仮説は次のように定式化されます。

• 帰無仮説 (H₀): グループ平均間に有意差がないことを前提としています。
• 対立仮説 (H₁): グループ平均間に有意な差があることを示唆します。

解釈

• p 値が有意水準 (通常は 0.05 に設定) を下回る場合、帰無仮説は棄却され、有意差があることが示されます。
• 逆に、有意水準を超える p 値は帰無仮説を棄却できません。

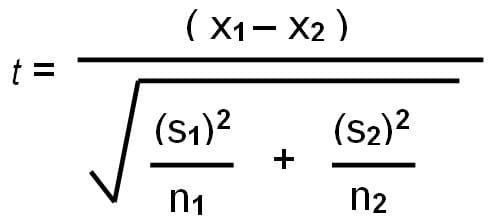
Z-テストとは何ですか?

Z 検定は、サンプル平均と母集団平均の間、または 2 つの独立したサンプルの平均の間に有意な差があるかどうかを判断するために使用される統計手法です。これは、大きなサンプルサイズを扱う場合や母集団の標準偏差がわかっている場合に特に役立ちます。

Z テストの種類

1. 1 サンプル Z 検定:
   • 目的： かどうかを評価するには、 意味する 単一サンプルの平均値は既知の母集団平均値と大きく異なります。
   • 式： Z = (X̄ – μ) / (σ / √n)。ここで、X̄ は標本平均、μ は母集団平均、σ は母集団標準偏差、n は標本サイズです。
2. 2 サンプル Z 検定:
   • 目的： 2 つの独立したサンプルの平均を比較し、それらの間に有意な差があるかどうかを判断します。
   • 式： Z = (X̄₁ – X̄₂) / √(σ₁²/n₁ + σ₂²/n₂)、ここで、X̄₁ および X̄₂ は標本平均、σ1 および σ2 は標準偏差、n₁ および n₂ は標本サイズです。
3. 比率の Z 検定:
   • 目的： サンプル内のカテゴリ変数の割合が既知の母集団の割合と大きく異なるかどうかを調べること。
   • 式： Z = (p̂ – p₀) / √(p₀(1 – p₀)/n)、ここで、p̂ はサンプルの割合、p₀ は母集団の割合、n はサンプル サイズです。

Z 検定による仮説検定

仮説検定には、帰無仮説 (H₀) と対立仮説 (H₁ または Ha) を設定することが含まれます。

• 帰無仮説 (H₀): 大きな違いや影響はないと考えられます。
• 対立仮説 (H₁ または Ha): 重大な違いまたは効果を主張します。

帰無仮説を棄却するかどうかの決定は、計算された Z 統計量と選択された有意水準 (α) に基づいて行われます。計算された p 値が α より小さい場合、帰無仮説は棄却され、統計的有意性が示されます。

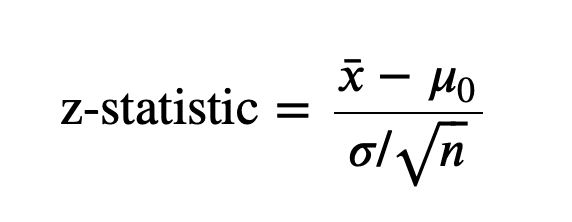
T検定とZ検定の主な違い

1. サンプルサイズ：
   • T 検定: 通常、サンプル サイズが小さい場合 (<30)、または母集団の標準偏差が不明な場合に使用されます。
   • Z 検定: 通常、サンプル サイズが大きい (>30) 場合、および母集団の標準偏差が既知であるか、正確に推定できる場合に使用されます。
2. 母集団標準偏差:
   • T 検定: 母集団標準偏差の知識は必要ありません。 サンプルから推定することができます。
   • Z 検定: 母集団の標準偏差に関する知識、または標本からそれを推定するのに十分な大きさの標本サイズが必要です。
3. 式：
   • T 検定: T 検定の式には、サンプル平均、サンプル標準偏差、サンプルサイズ、およびオプションで母集団平均が含まれます。
   • Z 検定: Z 検定の式には、サンプル平均、母集団平均、母標準偏差、サンプル サイズが含まれます。
4. 自由度：
   • T 検定: 1 サンプルの T 検定には (n – 1) の自由度を使用し、XNUMX サンプルの T 検定には (n – XNUMX) の自由度を使用します (n はサンプル サイズ)。
   • Z 検定: XNUMX サンプルの Z 検定に n 自由度を使用します。
5. ディストリビューション：
   • T 検定: 標準の正規 (z) 分布と比較して裾が重い t 分布に従います。
   • Z 検定: 標準の正規 (z) 分布に従います。
6. 分散の仮定:
   • T 検定: 標本分散が母集団分散の不偏推定量であると仮定します。
   • Z 検定: 母集団の分散が既知であるか、サンプルから合理的に推定できることを前提としています。
7. 使用事例：
   • T 検定: サンプルサイズが小さい場合、母集団の標準偏差が不明な場合、またはサンプルサイズが小さい XNUMX つのグループの平均を比較する場合に一般的に使用されます。
   • Z 検定: サンプルサイズが大きい場合、母集団の標準偏差が既知である場合、またはサンプルサイズが大きい XNUMX つのグループの平均を比較する場合に一般的に使用されます。
8. 統計ソフトウェア:
   • T 検定: 一般的に、R、Python、統計計算機などの統計ソフトウェアを使用して実行されます。
   • Z 検定: また、一般的には、R、Python、統計計算機などの統計ソフトウェアを使用して実行されます。

最終更新日 : 25 年 2024 月 XNUMX 日