В статистике корреляции подразделяются на две формы, т. е. двумерные и частные корреляции. Корреляция — это степень и направление связи двух переменных, другими словами, насколько эффективно одна может быть получена из другой.
Общие отношения между двумя переменными могут быть положительными, оптимистичными или криволинейными. Для ее измерения и выражения используются числовые шкалы. Корреляции называются положительными, когда они увеличиваются одновременно, и отрицательными, когда их значение уменьшается.
Основные выводы
- Двумерная корреляция исследует связь между двумя переменными, тогда как частичная корреляция оценивает связь после контроля одной или нескольких переменных.
- На двумерную корреляцию могут влиять искажающие факторы, но частичная корреляция устраняет их влияние, чтобы обеспечить более четкое понимание.
- Частичная корреляция более сложна для расчета и интерпретации, чем двумерная корреляция, и требует дополнительных статистических методов.
Двумерная и частичная корреляция
Двумерный корреляция это статистический метод, используемый для измерения силы и направления линейной зависимости между двумя переменными. Частичная корреляция — это статистический метод, используемый для измерения взаимосвязи между двумя переменными с учетом влияния некоторых переменных.
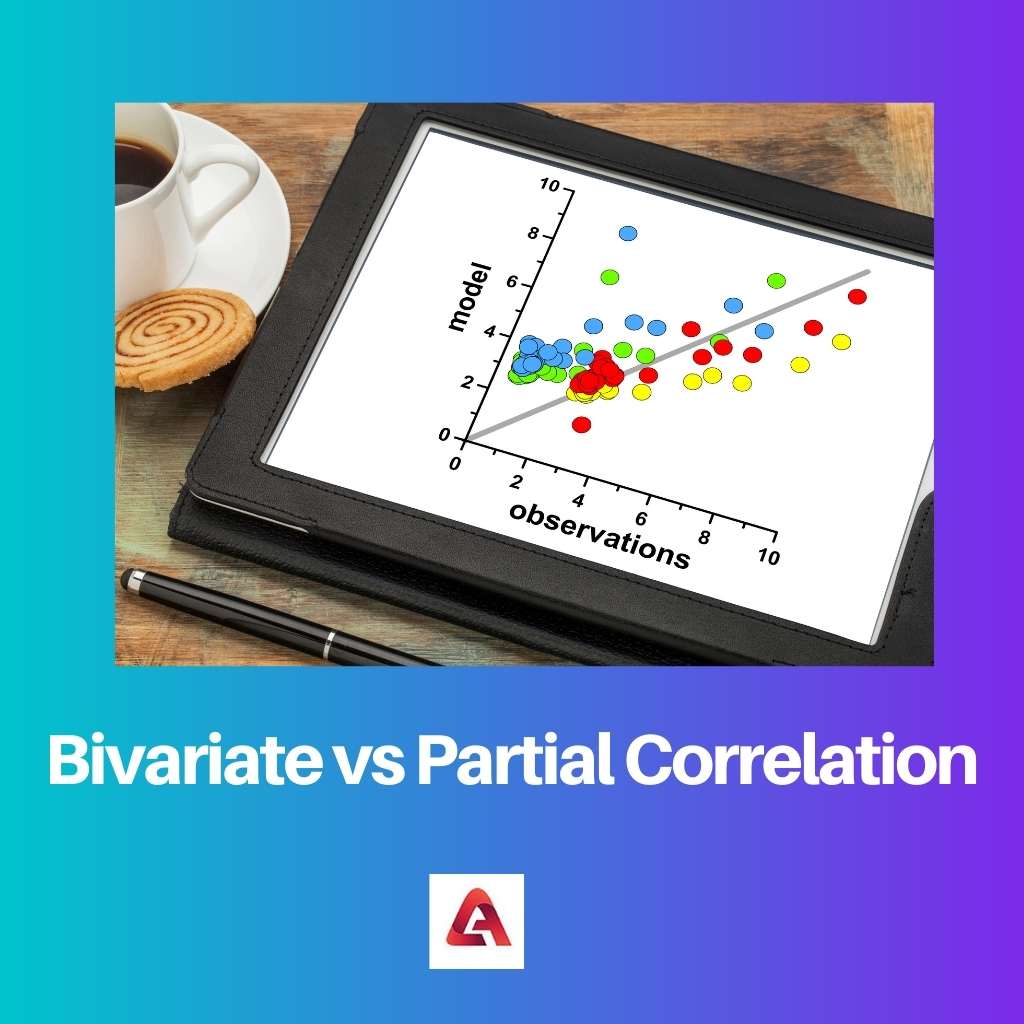
Двумерная корреляция применяется для определения того, связаны ли две переменные. Он оценивает, как одновременно изменяются переменные.
Исследование с помощью двумерного метода помогает одновременно исследовать несколько элементов. Этот анализ пытается точно определить линейную зависимость между двумя переменными.
Частичная корреляция отличается от двумерной; он удаляет дополнительную переменную, чтобы обозначить корреляцию между двумя переменными. Этот метод помогает вычислить корреляцию между переменными, исключая влияние третьей переменной.
Он может превосходно работать в множественной регрессии. При этом типе корреляции накапливаются ценные данные для обнаружения скрытых связей и выявления корреляций.
Сравнительная таблица
Что такое двумерная корреляция?
Двумерная корреляция подходит для оценки простых предположений о связи и причинности. Двумерный анализ идет дальше в описании; он одновременно исследует многочисленные взаимосвязи между несколькими переменными.
Длина и ширина объекта — два примера двумерной ассоциации.
Когда одна переменная является произвольной или любую переменную трудно измерить, двумерная корреляция может помочь в понимании и прогнозировании результатов других переменных.
Двумерную корреляцию можно измерить с помощью различных тестов, таких как диаграмма рассеяния и тест корреляции продукта-момента Пирсона. Корреляционная матрица используется для представления результатов тестирования этой корреляции.
Корреляция — это единичное значение от -1 до +1, отражающее интенсивность связи или совпадения двух переменных.
Эта статистика, которая количественно определяет силу связи, известна как коэффициент корреляции и обычно обозначается буквой «r».
Коэффициент корреляции Пирсона «продукт-момент» — это второе название коэффициента корреляции между двумя переменными непрерывного уровня.
Положительное значение r означает положительную связь между двумя переменными (чем лучше A, тем лучше B). Напротив, отрицательное значение r означает отрицательную связь (чем больше A, тем меньше B).
Значение корреляции, равное 0, показывает отсутствие связи между компонентами. Корреляции, с другой стороны, ограничены линейными отношениями между переменными. Нелинейная зависимость может существовать, даже если коэффициент корреляции равен нулю.
Что такое частичная корреляция?
Когда влияние связанных переменных исключается из уравнения, корреляция между двумя переменными называется частичной корреляцией. Он превосходно работает в множественной регрессии.
Это метод объяснения связи между независимые переменные, игнорируя влияние другой переменной внутри отношения.
Он накапливает переменные, чтобы определить, демонстрируют ли они коллективное поведение. Частичная корреляция полезна для обнаружения скрытых связей и выявления ложных корреляций.
Связь между весом и ростом человека после контроля значения возраста иллюстрирует частичную корреляцию.
Предположим, мы хотим определить, насколько сильна связь между двумя интересующими нас переменными, используя их коэффициент корреляции. В этом случае это даст вводящие в заблуждение результаты, если есть еще одна переменная, которая является загадочной переменной и численно связана с обеими интересующими переменными.
Контроль влияющей переменной, который достигается путем расчета коэффициента частичной корреляции, может помочь избежать вводящих в заблуждение данных.
Вот почему множественная регрессия включает дополнительные правые переменные; однако, несмотря на то, что многочисленные регрессии дают результаты, которые не предвзяты в отношении размера воздействия, они не дают числового значения степени взаимосвязи между двумя интересующими переменными.
Частная корреляция имеет значение от –1 до 1. Значение –1 обозначает идеальную отрицательную корреляцию с учетом конкретных переменных, 1 указывает на идеальную положительную линейную зависимость, а 0 указывает на отсутствие линейной зависимости.
Основные различия между двумерной и частичной корреляцией
- Двумерная корреляция определяет, связаны ли две переменные или нет. С другой стороны, частичная корреляция используется для количественной оценки взаимосвязи после поправки на другие переменные.
- Двумерная корреляция — это измерение или анализ двух переменных. Однако частичная корреляция оценивает степень присутствия дополнительных факторов.
- Такие переменные, как X и Y, часто используются в двумерной корреляции. Частичная корреляция предполагает использование случайных величин, таких как X и Y, X и Z или Y и Z.
- Символом двумерной корреляции является «r» Пирсона (R), а для частичной корреляции — «rYX.W».
- Двумерная корреляция используется для расчета коэффициента корреляции, который показывает степень связи между двумя линейными переменными. После корректировки одной или нескольких переменных для получения коэффициентов корреляции используется частичная корреляция.
- https://onlinelibrary.wiley.com/doi/abs/10.1002/jrsm.1126
- https://www.tandfonline.com/doi/abs/10.1207/s15327906mbr3803_02
Последнее обновление: 13 июля 2023 г.
Я приложил столько усилий, чтобы написать этот пост в блоге, чтобы предоставить вам ценность. Это будет очень полезно для меня, если вы подумаете о том, чтобы поделиться им в социальных сетях или со своими друзьями/родными. ДЕЛИТЬСЯ ♥️
Эмма Смит имеет степень магистра английского языка в колледже Ирвин-Вэлли. Она работает журналистом с 2002 года, пишет статьи об английском языке, спорте и праве. Подробнее обо мне на ней био страница.
В статье представлено тщательное и содержательное сравнение двумерных и частичных корреляций. Использование наглядных примеров лучше иллюстрирует эти статистические методы. Предоставленные ссылки также помогают подтвердить изложенные факты. В целом, это было очень познавательное чтение.
Ты прав. В статье дается исчерпывающее объяснение. Используемые примеры облегчили понимание концепций.
Согласованный. Углубленное сравнение и четкие объяснения делают его отличным ресурсом для статистиков и исследователей.
Это информативная статья. Он обеспечивает четкое различие между двумерными и частичными корреляциями, что важно для исследователей. Объяснения и примеры помогают эффективно усвоить концепции.
В статье дается подробное объяснение в сочетании с практическими примерами и четким сравнением. Это полезный ресурс для тех, кто хочет получить полное представление о двумерных и частичных корреляциях.
Абсолютно. Подробный и иллюстративный подход статьи помогает понять эти статистические методы.
Действительно, статья предлагает познавательное чтение для статистиков и исследователей. Приведенные примеры повышают ясность понятий.
Статья проделала похвальную работу по разъяснению сложных концепций двумерных и частных корреляций. Глубина объяснений и сравнительная таблица делают его ценным ресурсом для тех, кто занимается статистическими исследованиями.
Представленные сравнения кратки и помогают понять различия между двумерными и частными корреляциями. Статья не только объясняет концепции, но и углубляется в их конкретные применения в статистическом анализе.
Сравнения двумерных и частных корреляций весьма поучительны, а статья служит ценным руководством для понимания этих статистических методов.