Т-тест против Z-теста: разница и сравнение

T-критерий используется для сравнения выборочных средних, когда стандартное отклонение генеральной совокупности неизвестно или при работе с небольшими размерами выборки, тогда как z-критерий подходит, когда стандартное отклонение генеральной совокупности известно и размеры выборки достаточно велики.

Основные выводы

1. T-тесты используются для сравнения средних значений двух групп, когда стандартное отклонение совокупности неизвестно, а Z-тесты используются, когда известно стандартное отклонение совокупности и размер выборки большой.
2. T-тесты основаны на t-распределении, которое используется для меньших размеров выборки и неизвестных стандартных отклонений населения, тогда как Z-тесты используют стандартное нормальное распределение.
3. На практике t-тесты более распространены из-за редкости известных стандартных отклонений генеральной совокупности. В то же время Z-тесты предназначены для ситуаций с большими размерами выборки и известными параметрами совокупности.

Т-тест против Z-теста

Z-тест используется, когда известны среднее значение совокупности и стандартное отклонение, предполагается, что население распределено нормально. Критерий Стьюдента используется, когда стандартное отклонение популяции неизвестно и должно быть оценено по образец данные. Т-тест предполагает, что выборка имеет нормальное распределение.

T-тест лучше всего подходит для задач с ограниченным размером выборки, тогда как Z-тест лучше всего подходит для задач с большими размерами выборки.

Сравнительная таблица

Аспект	Т-тест	Z-тест
Примеры использования	Используется, когда размер выборки небольшой (<30) или стандартное отклонение генеральной совокупности неизвестно.	Используется, когда размер выборки велик (>30) и известно стандартное отклонение генеральной совокупности.
Размер образца	Подходит для небольших выборок.	Подходит для больших объемов выборок.
Формула	t = (x̄ – µ) / (s / √n)	z = (x̄ – µ) / (σ / √n)
Параметры популяции	Обычно используется, когда параметры совокупности (среднее значение и стандартное отклонение) неизвестны.	Обычно используется, когда параметры совокупности (среднее значение и стандартное отклонение) известны или оценены.
Степени свободы	Использует n-1 степеней свободы (где n — размер выборки) для двухвыборочного t-критерия.	Использует n степеней свободы для одновыборочного z-критерия.
Допущение дисперсии	Предполагается, что выборочная дисперсия является несмещенной оценкой генеральной дисперсии.	Предполагается, что генеральная дисперсия известна или может быть разумно оценена на основе выборки.
Распределение	Следует t-распределению, которое имеет более тяжелые хвосты по сравнению со стандартным нормальным (z) распределением.	Следует стандартному нормальному (z) распределению.
Пример	Проверка того, значительно ли различаются средние баллы тестов двух разных групп, когда размеры выборки невелики и стандартные отклонения популяции неизвестны.	Проверка того, значительно ли средний рост населения отличается от известного значения, когда размер выборки велик и известно стандартное отклонение населения.
Статистическое программное обеспечение	Обычно выполняется с использованием такого программного обеспечения, как R, Python или статистических калькуляторов.	Обычно выполняется с использованием такого программного обеспечения, как R, Python или статистических калькуляторов.

Что такое Т-тест?

T-тест — это статистический метод, используемый для сравнения средних значений двух групп и определения наличия между ними значительной разницы. Его обычно используют при проверке гипотез, когда данные подчиняются нормальному распределению.

Виды Т-тестов

1. Независимые образцы Т-тест:
   • Используется при сравнении средних двух независимых групп.
   • Предположение: данные в каждой группе нормально распределены, а дисперсии примерно равны.
2. Т-тест для парных образцов:
   • Применяется при сравнении средних значений двух связанных групп, например, до и после измерений.
   • Предположение: различия между парными наблюдениями нормально распределены.

Гипотезы в T-тесте

В Т-тесте гипотезы формулируются следующим образом:

• Нулевая гипотеза (H₀): Предполагается отсутствие существенной разницы между групповыми средними значениями.
• Альтернативная гипотеза (H₁): Предполагает существенную разницу между групповыми средствами.

Интерпретация

• Если значение p ниже уровня значимости (обычно устанавливаемого на уровне 0.05), нулевая гипотеза отклоняется, что указывает на значительную разницу.
• И наоборот, значение p выше уровня значимости не может отвергнуть нулевую гипотезу.

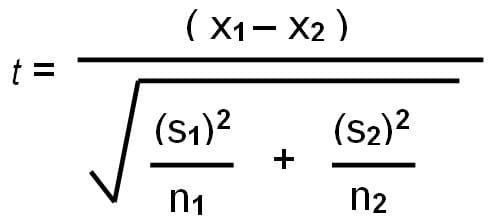
Что такое Z-тест?

Z-тест — это статистический метод, используемый для определения наличия значительной разницы между средними значениями выборки и совокупности или между средними значениями двух независимых выборок. Это особенно полезно при работе с большими размерами выборки и когда известно стандартное отклонение генеральной совокупности.

Виды Z-тестов

1. Одновыборочный Z-тест:
   • Цель: Чтобы оценить, является ли значить одной выборки значительно отличается от известного среднего значения популяции.
   • Формула: Z = (X̄ – μ) / (σ / √n), где X̄ — среднее значение выборки, μ — среднее значение генеральной совокупности, σ — стандартное отклонение генеральной совокупности, а n — размер выборки.
2. Двухвыборочный Z-тест:
   • Цель: Сравнить средние значения двух независимых выборок и определить, есть ли между ними значительная разница.
   • Формула: Z = (X̄₁ – X̄₂) / √(σ₁²/n₁ + σ₂²/n₂), где X̄₁ и X̄₂ — средние значения выборки, σ₁ и σ₂ — стандартные отклонения, а n₁ и n₂ — размеры выборки.
3. Z-тест для пропорций:
   • Цель: Проверить, значительно ли отличается доля категориальной переменной в выборке от известной доли в совокупности.
   • Формула: Z = (p̂ – p₀) / √(p₀(1 – p₀)/n), где p̂ — доля выборки, p₀ — доля населения, а n — размер выборки.

Проверка гипотез с помощью Z-Test

Проверка гипотезы включает в себя создание нулевой гипотезы (H₀) и альтернативной гипотезы (H₁ или Ha):

• Нулевая гипотеза (H₀): Предполагается отсутствие существенной разницы или эффекта.
• Альтернативная гипотеза (H₁ или Ha): Заявляет о существенной разнице или эффекте.

Решение об отклонении нулевой гипотезы принимается на основе рассчитанной Z-статистики и выбранного уровня значимости (α). Если рассчитанное значение p меньше α, нулевая гипотеза отклоняется, что указывает на статистическую значимость.

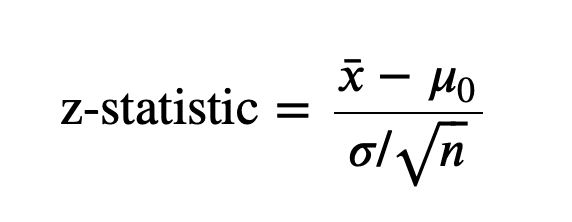
Основные различия между T-тестом и Z-тестом

1. Размер образца:
   • Т-тест: Обычно используется, когда размер выборки небольшой (<30) или когда стандартное отклонение генеральной совокупности неизвестно.
   • Z-тест: Обычно используется, когда размер выборки велик (>30) и когда стандартное отклонение генеральной совокупности известно или может быть точно оценено.
2. Стандартное отклонение населения:
   • Т-тест: Не требует знания стандартного отклонения генеральной совокупности; он может оценить это по выборке.
   • Z-тест: Требуется знание стандартного отклонения генеральной совокупности или достаточно большой размер выборки, чтобы оценить его на основе выборки.
3. Формула:
   • Т-тест: Формула Т-критерия включает в себя среднее значение выборки, стандартное отклонение выборки, размер выборки и, необязательно, среднее значение генеральной совокупности.
   • Z-тест: Формула Z-теста включает в себя среднее выборочное, среднее генеральное, стандартное отклонение генеральной совокупности и размер выборки.
4. Степени свободы:
   • Т-тест: Использует (n – 1) степеней свободы для двухвыборочного Т-критерия и (n – 1) степеней свободы для одновыборочного Т-критерия (где n — размер выборки).
   • Z-тест: Использует n степеней свободы для одновыборочного Z-теста.
5. Распространение:
   • Т-тест: Следует t-распределению с более тяжелыми хвостами по сравнению со стандартным нормальным (z) распределением.
   • Z-тест: Следует стандартному нормальному (z) распределению.
6. Допущение дисперсии:
   • Т-тест: Предполагается, что выборочная дисперсия является несмещенной оценкой генеральной дисперсии.
   • Z-тест: Предполагается, что генеральная дисперсия известна или может быть разумно оценена на основе выборки.
7. Случаи использования:
   • Т-тест: Обычно используется, когда размер выборки небольшой, стандартное отклонение генеральной совокупности неизвестно или при сравнении средних значений двух групп с небольшими размерами выборки.
   • Z-тест: Обычно используется, когда размер выборки велик, когда известно стандартное отклонение генеральной совокупности, или при сравнении средних значений двух групп с большими размерами выборки.
8. Статистическое программное обеспечение:
   • Т-тест: Обычно выполняется с использованием статистического программного обеспечения, такого как R, Python или статистических калькуляторов.
   • Z-тест: Также обычно выполняется с использованием статистического программного обеспечения, такого как R, Python или статистических калькуляторов.

Последнее обновление: 25 февраля 2024 г.