T-test vs Z-test: Perbedaan dan Perbandingan

Uji-t digunakan untuk membandingkan rata-rata sampel ketika simpangan baku populasi tidak diketahui atau bila ukuran sampelnya kecil, sedangkan uji z cocok bila simpangan baku populasi diketahui dan ukuran sampel cukup besar.

Pengambilan Kunci

1. Uji-t digunakan untuk membandingkan rata-rata dua kelompok ketika standar deviasi populasi tidak diketahui, sedangkan uji-Z digunakan ketika standar deviasi populasi diketahui, dan ukuran sampelnya besar.
2. Uji-t bergantung pada distribusi-t, yang digunakan untuk ukuran sampel yang lebih kecil dan standar deviasi populasi yang tidak diketahui, sedangkan uji-Z menggunakan distribusi normal baku.
3. Dalam praktiknya, uji-t lebih umum dilakukan karena jarangnya simpangan baku populasi yang diketahui. Pada saat yang sama, uji Z dicadangkan untuk situasi dengan ukuran sampel yang besar dan parameter populasi yang diketahui.

Uji-T vs uji-Z

Uji-Z digunakan ketika rata-rata populasi dan standar deviasi diketahui, diasumsikan bahwa populasi terdistribusi normal. Uji-t digunakan ketika standar deviasi populasi tidak diketahui dan harus diestimasi dari mencicipi data. Itu uji-t mengasumsikan bahwa sampel terdistribusi secara normal.

Uji-T paling baik untuk masalah dengan ukuran sampel terbatas, sedangkan uji-Z bekerja paling baik untuk masalah dengan ukuran sampel besar.

Tabel perbandingan

Aspek	Uji-T	Z-Tes
Gunakan kasing	Digunakan ketika ukuran sampel kecil (<30) atau deviasi standar populasi tidak diketahui.	Digunakan ketika ukuran sampel besar (>30) dan deviasi standar populasi diketahui.
Ukuran sampel	Cocok untuk ukuran sampel kecil.	Cocok untuk ukuran sampel besar.
Rumus	t = (x̄ – μ) / (s / √n)	z = (x̄ – μ) / (σ / √n)
Parameter populasi	Biasanya digunakan ketika parameter populasi (rata-rata dan deviasi standar) tidak diketahui.	Biasanya digunakan ketika parameter populasi (rata-rata dan deviasi standar) diketahui atau diperkirakan.
Derajat kebebasan	Menggunakan n-1 derajat kebebasan (di mana n adalah ukuran sampel) untuk uji-t dua sampel.	Menggunakan n derajat kebebasan untuk uji-z satu sampel.
Asumsi varians	Diasumsikan bahwa varians sampel adalah penduga varians populasi yang tidak bias.	Diasumsikan bahwa varians populasi diketahui atau dapat diperkirakan secara wajar dari sampel.
Distribusi	Mengikuti distribusi t, yang memiliki ekor lebih berat dibandingkan distribusi normal standar (z).	Mengikuti distribusi normal standar (z).
Contoh	Menguji apakah nilai tes rata-rata dari dua kelompok berbeda berbeda secara signifikan ketika ukuran sampel kecil dan standar deviasi populasi tidak diketahui.	Menguji apakah rata-rata tinggi badan suatu populasi berbeda secara signifikan dari nilai yang diketahui ketika ukuran sampel besar dan simpangan baku populasi diketahui.
Perangkat lunak statistik	Biasanya dilakukan menggunakan perangkat lunak seperti R, Python, atau kalkulator statistik.	Biasanya dilakukan menggunakan perangkat lunak seperti R, Python, atau kalkulator statistik.

Apa itu Uji-T?

Uji-t adalah metode statistik yang digunakan untuk membandingkan rata-rata dua kelompok dan menentukan apakah terdapat perbedaan yang signifikan di antara keduanya. Ini biasanya digunakan dalam pengujian hipotesis ketika data mengikuti distribusi normal.

Jenis Uji-T

1. Uji-T Sampel Independen:
   • Digunakan ketika membandingkan rata-rata dua kelompok independen.
   • Asumsi: Data di setiap kelompok terdistribusi normal dan variansnya kira-kira sama.
2. Uji-T Sampel Berpasangan:
   • Diterapkan ketika membandingkan rata-rata dua kelompok terkait, seperti sebelum dan sesudah pengukuran.
   • Asumsi: Perbedaan antara observasi berpasangan berdistribusi normal.

Hipotesis dalam Uji-T

Dalam Uji-T, hipotesis dirumuskan sebagai berikut:

• Hipotesis Nol (H₀): Mengasumsikan tidak ada perbedaan yang signifikan antara rata-rata kelompok.
• Hipotesis Alternatif (H₁): Menyarankan perbedaan yang signifikan antara rata-rata kelompok.

Interpretasi

• Jika nilai p berada di bawah tingkat signifikansi (biasanya ditetapkan sebesar 0.05), hipotesis nol ditolak, yang menunjukkan adanya perbedaan yang signifikan.
• Sebaliknya, nilai p di atas tingkat signifikansi gagal menolak hipotesis nol.

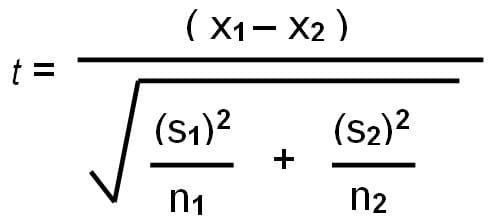
Apa itu Uji-Z?

Uji Z adalah metode statistik yang digunakan untuk menentukan apakah terdapat perbedaan yang signifikan antara rata-rata sampel dan populasi, atau antara rata-rata dua sampel independen. Hal ini sangat berguna ketika berhadapan dengan ukuran sampel yang besar dan ketika deviasi standar populasi diketahui.

Jenis Tes Z

1. Uji Z Satu Sampel:
   • Tujuan: Untuk menilai apakah berarti sampel tunggal berbeda secara signifikan dari rata-rata populasi yang diketahui.
   • Formula: Z = (X̄ – μ) / (σ / √n), dengan X̄ adalah mean sampel, μ adalah mean populasi, σ adalah simpangan baku populasi, dan n adalah ukuran sampel.
2. Uji Z Dua Sampel:
   • Tujuan: Untuk membandingkan rata-rata dua sampel independen dan menentukan apakah terdapat perbedaan signifikan di antara keduanya.
   • Formula: Z = (X̄₁ – X̄₂) / √(σ₁²/n₁ + σ₂²/n₂), dengan X̄₁ dan X̄₂ adalah mean sampel, σ₁ dan σ₂ adalah simpangan baku, dan n₁ dan n₂ adalah ukuran sampel.
3. Uji-Z untuk Proporsi:
   • Tujuan: Untuk menguji apakah proporsi suatu variabel kategori dalam suatu sampel berbeda secara signifikan dari proporsi populasi yang diketahui.
   • Formula: Z = (p̂ – p₀) / √(p₀(1 – p₀)/n), dengan p̂ adalah proporsi sampel, p₀ adalah proporsi populasi, dan n adalah ukuran sampel.

Pengujian Hipotesis dengan Uji Z

Pengujian hipotesis melibatkan penetapan hipotesis nol (H₀) dan hipotesis alternatif (H₁ atau Ha):

• Hipotesis Nol (H₀): Mengasumsikan tidak ada perbedaan atau pengaruh yang signifikan.
• Hipotesis Alternatif (H₁ atau Ha): Mengklaim perbedaan atau efek yang signifikan.

Keputusan untuk menolak hipotesis nol didasarkan pada statistik Z yang dihitung dan tingkat signifikansi yang dipilih (α). Jika nilai p yang dihitung kurang dari α, hipotesis nol ditolak, yang menunjukkan signifikansi statistik.

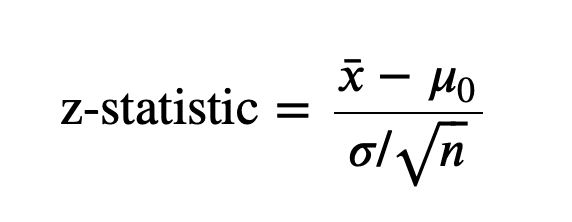
Perbedaan Utama Antara Uji-T dan Uji-Z

1. Ukuran sampel:
   • Uji-T: Biasanya digunakan ketika ukuran sampel kecil (<30) atau ketika standar deviasi populasi tidak diketahui.
   • Uji-Z: Biasanya digunakan ketika ukuran sampel besar (>30) dan ketika deviasi standar populasi diketahui atau dapat diperkirakan secara akurat.
2. Deviasi Standar Populasi:
   • Uji-T: Tidak memerlukan pengetahuan tentang simpangan baku populasi; ia dapat memperkirakannya dari sampel.
   • Uji-Z: Memerlukan pengetahuan tentang deviasi standar populasi atau ukuran sampel yang cukup besar untuk memperkirakannya dari sampel.
3. Formula:
   • Uji-T: Rumus uji-T melibatkan mean sampel, deviasi standar sampel, ukuran sampel, dan, opsional, mean populasi.
   • Uji-Z: Rumus uji Z melibatkan mean sampel, mean populasi, deviasi standar populasi, dan ukuran sampel.
4. Derajat kebebasan:
   • Uji-T: Menggunakan (n – 1) derajat kebebasan untuk uji T dua sampel dan (n – 1) derajat kebebasan untuk uji T satu sampel (di mana n adalah ukuran sampel).
   • Uji-Z: Menggunakan n derajat kebebasan untuk uji Z satu sampel.
5. Distribusi:
   • Uji-T: Mengikuti distribusi t dengan ekor yang lebih berat dibandingkan dengan distribusi normal standar (z).
   • Uji-Z: Mengikuti distribusi normal standar (z).
6. Asumsi Varians:
   • Uji-T: Diasumsikan bahwa varians sampel adalah penduga varians populasi yang tidak bias.
   • Uji-Z: Diasumsikan bahwa varians populasi diketahui atau dapat diperkirakan secara wajar dari sampel.
7. Gunakan Kasus:
   • Uji-T: Umumnya digunakan ketika ukuran sampel kecil, standar deviasi populasi tidak diketahui, atau ketika membandingkan rata-rata dua kelompok dengan ukuran sampel kecil.
   • Uji-Z: Umumnya digunakan ketika ukuran sampel besar, deviasi standar populasi diketahui, atau ketika membandingkan rata-rata dua kelompok dengan ukuran sampel besar.
8. Perangkat Lunak Statistik:
   • Uji-T: Biasanya dilakukan menggunakan perangkat lunak statistik seperti R, Python, atau kalkulator statistik.
   • Uji-Z: Biasanya juga dilakukan menggunakan perangkat lunak statistik seperti R, Python, atau kalkulator statistik.

Terakhir Diperbarui : 25 Februari 2024