Калькулятор дисперсии

Инструкция по применению

• Введите значения данных через запятую в поле «Введите данные».
• Выберите тип расчета (Выборка или Популяция) с помощью переключателей.
• Нажмите «Рассчитать», чтобы рассчитать дисперсию.
• Просмотрите результаты, среднее значение, визуализацию данных, историю вычислений и этапы расчета ниже.
• Нажмите «Очистить», чтобы сбросить настройки инструмента и ввести новые данные.
• Нажмите «Копировать результаты», чтобы скопировать рассчитанную дисперсию в буфер обмена.

Введите данные (через запятую):

Выберите тип расчета:

Образец

Население

Рассчитать Сбросить Копировать результаты

Среднее (среднее):

Визуализация данных:

История расчетов:

Шаги расчета:

Дисперсия — это статистическая мера, которая описывает, насколько данные в наборе отличаются от среднего значения. Это важное понятие в статистике и теории вероятностей. Калькулятор дисперсии — это инструмент, который помогает вычислить дисперсию набора данных. В этой статье мы обсудим концепции, формулы, преимущества, интересные факты и варианты использования калькулятора дисперсии.

концепции

Отклонение набора данных рассчитывается путем взятия среднего значения квадратов разностей между каждой точкой данных и средним значением. Формула расчета дисперсии выглядит следующим образом:

где:

• σ2 — дисперсия
• xi — значение i-й точки данных
• μ — среднее значение всех точек данных
• n — общее количество точек данных

Дисперсия говорит нам, насколько данные разбросаны по отношению к среднему значению. Высокая дисперсия указывает на то, что точки данных далеки от среднего значения, а низкая дисперсия указывает на то, что точки данных близки к среднему значению.

Формулы

Калькулятор дисперсии использует две разные формулы для расчета дисперсии в зависимости от того, есть ли у вас данные по всей совокупности или по выборке.

Дисперсия населения

Собрав данные от каждого интересующего вас члена генеральной совокупности, вы можете получить точное значение дисперсии генеральной совокупности. Формула генеральной дисперсии выглядит следующим образом:

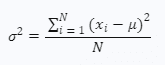
где:

• σ2 - популяционная дисперсия
• xi — значение i-й точки данных
• μ — среднее значение всех точек данных в совокупности.
• N — общее количество точек данных в совокупности

Выборочная дисперсия

Когда вы собираете данные из выборки, вы используете выборочную дисперсию, чтобы сделать оценки или выводы о генеральной дисперсии. Формула выборочной дисперсии выглядит следующим образом:

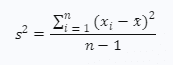
где:

• s2 — выборочная дисперсия
• xi — значение i-й точки данных
• xˉ — среднее значение всех точек данных в выборке.
• n — общее количество точек данных в выборке

Преимущества

Калькулятор дисперсии имеет ряд преимуществ:

1. Это помогает определить, насколько разбросан набор данных.
2. Он дает оценку того, насколько сильно варьируется набор данных.
3. Это помогает выявить выбросы в наборе данных.
4. Это помогает выявить закономерности в наборе данных.

Интересные факты

Вот несколько интересных фактов о дисперсии:

1. Дисперсия была впервые введена Рональдом Фишером в 1918 году.
2. Дисперсия может использоваться для расчета стандартного отклонения.
3. Дисперсия может использоваться для расчета ковариации.

Случаи использования

Вот несколько вариантов использования дисперсии:

1. В финансах его можно использовать для измерения риска.
2. В физике его можно использовать для измерения неопределенности.
3. В биологии его можно использовать для измерения генетических вариаций.

Последнее обновление: 25 ноября 2023 г.