Hai nửa đường thẳng hay còn gọi là các tia gặp nhau tại một điểm chung tạo ra khoảng cách giữa chúng. Một góc có thể được sử dụng để đo không gian này gần điểm cuối.
Các góc được mô tả là có tay và chân, trong khi đỉnh của chúng được mô tả là điểm cuối. Các phép đo radian và độ đều được sử dụng để mô tả các góc.
Góc là một khái niệm quan trọng có thể được sử dụng theo nhiều cách khác nhau trong cả toán học và vật lý. Các góc bổ sung và bổ sung là hai thuật ngữ được sử dụng rộng rãi.
Hiểu biết sâu sắc về ý nghĩa của những thuật ngữ này có thể giúp một cá nhân giải quyết rất nhiều vấn đề.
Chìa khóa chính
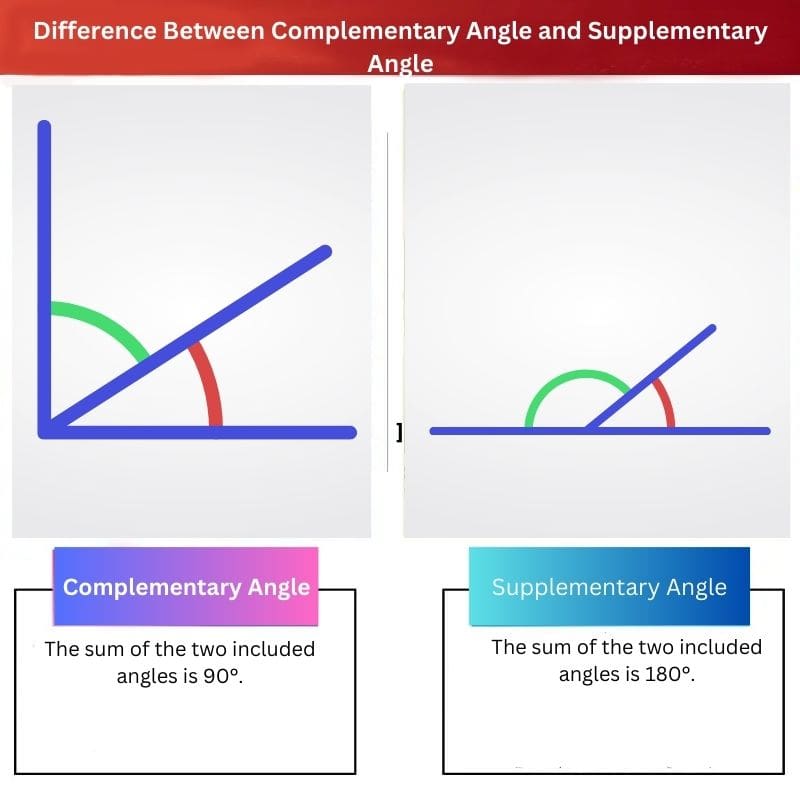
- Các góc bù nhau có tổng bằng 90 độ, trong khi các góc bù nhau có tổng bằng 180 độ.
- Các góc bổ sung được sử dụng trong các tam giác vuông, trong khi các góc bổ sung thường xuất hiện theo cặp tuyến tính.
- Hai góc có thể bổ sung hoặc bổ sung cho nhau, nhưng không đồng thời, vì chúng biểu thị các mối quan hệ góc khác nhau.
Góc bổ sung vs Góc bổ sung
Góc bù nhau tạo bởi hai góc đối đỉnh bổ thể nhau. Chúng tạo thành một góc vuông với nhau mà tổng các góc của chúng bằng 90 độ. Góc phụ tạo bởi hai góc phụ nhau. Chúng tạo thành một góc thẳng với nhau mà tổng các góc của chúng bằng 180 độ.
Các góc bù nhau được tạo thành khi tổng của một cặp góc bằng 90°. Một góc vuông được hình thành khi hai góc kề bù với nhau.
Ví dụ, hai góc có số đo lần lượt là 65° và 25° có thể coi là bù nhau vì tổng của chúng bằng 90°.
Bất cứ khi nào tổng của hai góc bằng chính xác 180 °, chúng được gọi là các góc bổ sung. Các góc thẳng được tạo thành bằng cách nối các góc phụ với nhau.
Ví dụ: nếu hai góc có số đo lần lượt là 110° và 70°, chúng có thể được coi là các góc phụ nhau vì tổng của chúng bằng 180°.
Bảng so sánh
| Các thông số so sánh | Góc bổ sung | Góc bổ sung |
|---|---|---|
| Tổng các góc theo độ | Tổng của hai góc xen giữa là 90°. | Tổng của hai góc xen giữa là 180°. |
| Tổng các góc trong π | Tổng hai góc xen giữa là π/2. | Tổng hai góc xen giữa là π. |
| Mô tả các góc | Cả hai góc liên quan đều nhọn, nghĩa là chúng nhỏ hơn 90°. | Một góc nhọn và góc kia tù, nghĩa là một góc nhỏ hơn 90° và góc kia lớn hơn 90°. |
| các góc bằng nhau | Nếu hai góc kề bù bằng nhau thì chúng bằng nhau 45°. | Nếu hai góc kề bù bằng nhau thì mỗi góc bằng 90°. |
| Cơ sở của các góc | Đáy của các góc bù nhau tạo thành một góc vuông. | Đáy của các góc phụ nhau tạo thành một đường thẳng. |
Góc bù là gì?
Khi tổng hai góc bằng 90° gọi là hai góc bù nhau. Nếu bất kỳ cặp góc nào có tổng thậm chí chênh lệch một độ so với 90°, chẳng hạn như 89° hoặc 90°, thì chúng không thể được xác định là các góc bù nhau.
Tổng của hai góc kề bù cần phải chính xác bằng 90°. Xét về π, tổng hai góc kề bù cần bằng π/2.
Vì vậy, ví dụ, ∠CDA = 70° và ∠BCD = 20° có thể được gọi là một cặp góc bù nhau vì tổng của chúng (70° + 20°) bằng chính xác 90°.
Góc nhỏ hơn 90° được gọi là góc nhọn. Vì các góc không thể âm nên cả hai góc tạo thành góc bù đều nhọn.
Nếu một góc bù nhau được chia thành hai phần bằng nhau, chúng ta sẽ có hai góc 45 ° mỗi góc. Do đó, hai góc bù nhau chỉ có thể bằng nhau nếu chúng có số đo bằng 45°.
Nếu đặt hai góc kề bù với nhau thì đáy của hai góc đó tạo thành góc vuông.
Góc phụ là gì?
Khi tổng hai góc bằng 180° gọi là góc phụ. Nếu bất kỳ cặp góc nào có tổng thậm chí chênh lệch một độ so với 180°, chẳng hạn như 179° hoặc 181°, thì chúng không thể được xác định là các góc bổ sung.
Tổng của hai góc bù nhau cần phải chính xác bằng 180°. Xét về π, tổng của hai góc kề bù cần phải bằng π.
Vì vậy, chẳng hạn, ∠ACD = 120° và ∠BCD = 60° có thể được gọi là một cặp góc phụ nhau vì tổng của chúng (120° + 60°) bằng chính xác 180°.
Các góc nhỏ hơn 180° nhưng lớn hơn 90° được gọi là góc tù. Do đó, trong số hai góc có liên quan, một trong các góc cần phải nhọn, trong khi góc kia cần phải tù.
Nghĩa là, một trong số chúng phải nhỏ hơn 90° trong khi cái kia phải lớn hơn 90°. Nếu chia một góc phụ thành hai phần bằng nhau thì ta được hai góc mỗi góc bằng 90°.
Do đó, hai góc phụ nhau chỉ có thể bằng nhau nếu cả hai đều có số đo bằng 90°. Nếu hai góc kề bù kề nhau thì đáy của cả hai góc là một đường thẳng.
Sự khác biệt chính giữa Góc bổ sung và Góc bổ sung
- Khi cộng hai góc kề bù với nhau thì có tổng bằng 90°, còn khi cộng hai góc kề bù với nhau thì có tổng bằng 180°.
- Tổng hai góc phụ nhau là π/2, nhưng tổng hai góc phụ nhau là π.
- Các góc bù nhau đều là các góc nhọn, nghĩa là cả hai đều nhỏ hơn 90°, trong khi các góc bù nhau có một góc nhọn và một góc tù, tức là một góc nhỏ hơn 90° và góc kia lớn hơn 90°.
- Nếu hai góc kề bù bằng nhau thì mỗi góc bằng nhau 45°, ngược lại nếu hai góc kề bù bằng nhau thì mỗi góc bằng 90°.
- Đáy của góc phụ tạo thành góc vuông, trong khi đáy của góc phụ tạo thành đường thẳng.
- https://www.igi-global.com/chapter/how-gaming-and-formative-assessment-contribute-to-learning-supplementary-and-complementary-angles/294960
- https://www.researchgate.net/profile/Leonor-Santos/publication/357205282_How_Gaming_and_Formative_Assessment_Contribute_to_Learning_Supplementary_and_Complementary_Angles/links/61c1a980c99c4b37eb1191c7/How-Gaming-and-Formative-Assessment-Contribute-to-Learning-Supplementary-and-Complementary-Angles.pdf
Cập nhật lần cuối: ngày 11 tháng 2023 năm XNUMX
Tôi đã nỗ lực rất nhiều để viết bài đăng trên blog này nhằm cung cấp giá trị cho bạn. Nó sẽ rất hữu ích cho tôi, nếu bạn cân nhắc chia sẻ nó trên mạng xã hội hoặc với bạn bè/gia đình của bạn. CHIA SẺ LÀ ♥️
Piyush Yadav đã dành 25 năm qua làm việc với tư cách là một nhà vật lý trong cộng đồng địa phương. Anh ấy là một nhà vật lý đam mê làm cho khoa học dễ tiếp cận hơn với độc giả của chúng tôi. Ông có bằng Cử nhân Khoa học Tự nhiên và Bằng Sau Đại học về Khoa học Môi trường. Bạn có thể đọc thêm về anh ấy trên trang sinh học.
