Tương quan so với hồi quy: Sự khác biệt và so sánh

Mối tương quan đo lường cường độ và hướng của mối quan hệ giữa hai biến số, cho biết chúng di chuyển cùng nhau như thế nào. Mặt khác, hồi quy mô hình hóa mối quan hệ giữa các biến, cho phép dự đoán và hiểu sự thay đổi của một biến này ảnh hưởng đến biến khác như thế nào, bao gồm cả việc định lượng tác động thông qua các hệ số và điểm chặn.

Chìa khóa chính

1. Tương quan đo lường cường độ và hướng của mối quan hệ giữa hai biến, trong khi hồi quy được sử dụng để dự đoán giá trị của một biến dựa trên giá trị của biến khác.
2. Tương quan không ngụ ý quan hệ nhân quả, trong khi hồi quy có thể giúp xác định mối quan hệ nhân quả.
3. Tương quan có thể được tính bằng một công thức đơn giản, trong khi hồi quy yêu cầu các mô hình toán học phức tạp hơn.

Tương quan so với hồi quy

Tương quan đề cập đến mức độ liên kết giữa hai biến. Hồi quy được sử dụng để mô hình hóa mối quan hệ giữa hai biến. Tương quan đo lường mức độ liên kết giữa hai biến, trong khi hồi quy mô hình hóa mối quan hệ giữa hai biến.

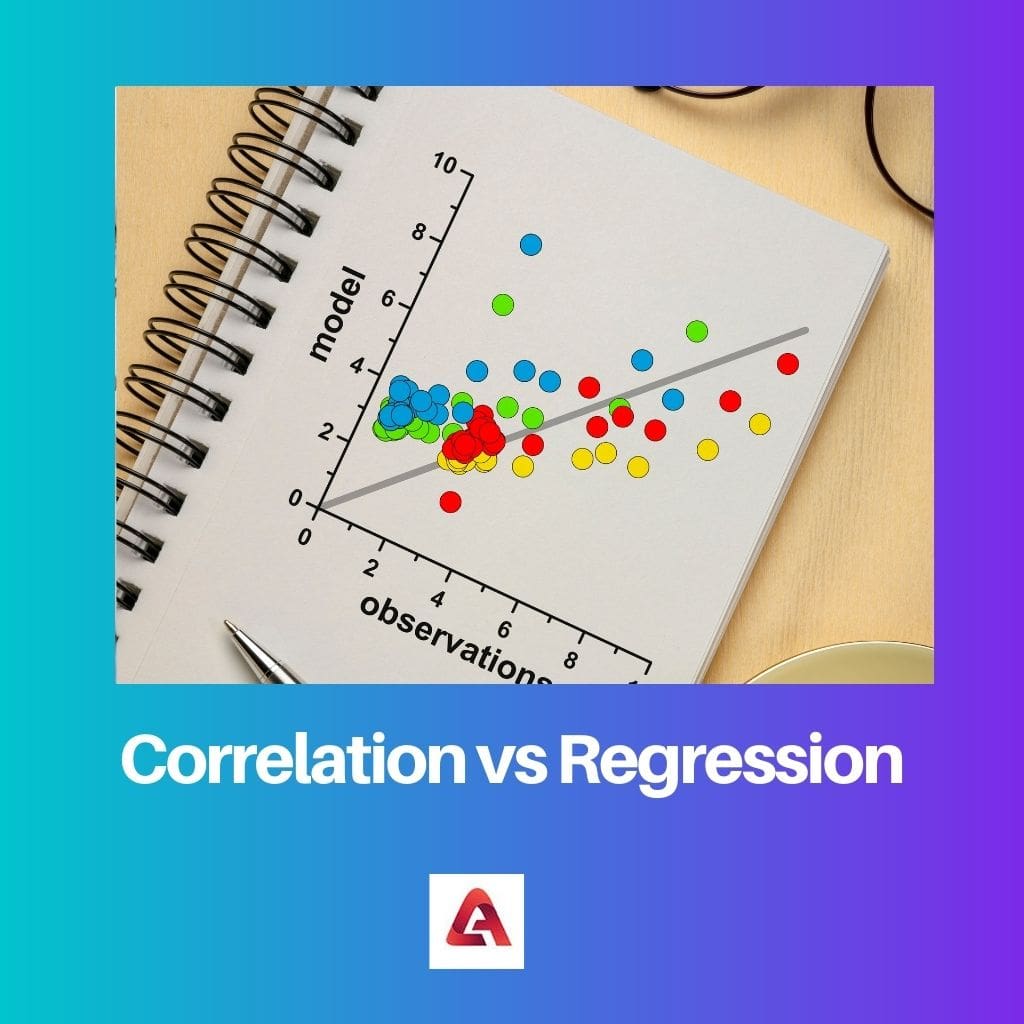
Mối quan hệ giữa hai biến khác nhau được đánh giá ban đầu. Hồi quy có vô số ứng dụng trực quan trong cuộc sống hàng ngày. Dưới đây là bảng so sánh kỹ lưỡng có thể giải thích thành công sự khác biệt giữa hai thuật ngữ.

Bảng so sánh

Đặc tính	Tương quan	Hồi quy
Mục đích	đo lường sức mạnh và hướng của mối quan hệ giữa hai biến	Mô hình sự phụ thuộc của một biến (phụ thuộc) vào một biến khác (độc lập)
Đầu ra	Một hệ số duy nhất (r) nằm trong khoảng từ -1 đến 1 (-1: âm hoàn toàn, 0: không có mối quan hệ, 1: dương hoàn toàn)	Một phương trình hoặc mô hình dự đoán giá trị của biến phụ thuộc dựa trên biến độc lập
quan hệ nhân quả	Không ngụ ý nhân quả	Có thể gợi ý nguyên nhân nhưng cần phân tích sâu hơn để xác nhận
Giả định	Yêu cầu tính tuyến tính và tính đồng nhất (phương sai bằng nhau) của dữ liệu	Các giả định chặt chẽ hơn, bao gồm tính quy tắc của phần dư (sai số)
Ứng dụng	Xác định xu hướng, hiểu mối quan hệ, khám phá dữ liệu	Dự đoán giá trị tương lai, đưa ra dự báo, đưa ra quyết định dựa trên dự đoán mô hình
Các ví dụ	Nghiên cứu mối tương quan giữa nhiệt độ và doanh số bán kem	Xây dựng mô hình dự đoán giá nhà theo quy mô, vị trí

Tương quan là gì?

Tương quan là một thước đo thống kê nhằm định lượng cường độ và hướng của mối quan hệ giữa hai biến định lượng. Nó đánh giá những thay đổi trong một biến có liên quan như thế nào với những thay đổi trong một biến khác.

Các loại tương quan

1. Tương quan Tích cực: Khi cả hai biến di chuyển theo cùng một hướng. Nghĩa là khi một biến tăng thì biến kia cũng có xu hướng tăng và ngược lại. Ví dụ: có thể có mối tương quan thuận giữa số giờ học và điểm thi.
2. Tương quan tiêu cực: Khi các biến di chuyển theo hướng ngược lại. Điều này có nghĩa là khi một biến tăng thì biến kia có xu hướng giảm và ngược lại. Một ví dụ có thể là mối quan hệ giữa nhiệt độ và doanh số bán quần áo mùa đông.
3. Không tương quan: Khi không có mối quan hệ rõ ràng giữa các biến. Những thay đổi trong một biến không dự đoán được những thay đổi trong biến kia. Điều này không hàm ý rằng các biến số không liên quan với nhau, chỉ là mối quan hệ của chúng không tuyến tính.

Đo tương quan

• r = +1 biểu thị mối tương quan dương hoàn hảo
• r = -1 biểu thị mối tương quan âm hoàn hảo
• r = 0 biểu thị không có mối tương quan

Các phương pháp khác để đo lường mối tương quan bao gồm hệ số tương quan xếp hạng của Spearman và hệ số tau của Kendall, được sử dụng cho dữ liệu thứ tự hoặc khi mối quan hệ giữa các biến không tuyến tính.

Hồi quy là gì?

Phân tích hồi quy là một phương pháp thống kê được sử dụng để kiểm tra mối quan hệ giữa một biến phụ thuộc (ký hiệu là “Y”) và một hoặc nhiều biến độc lập (ký hiệu là “X”). Nó cho phép chúng ta dự đoán giá trị của biến phụ thuộc dựa trên giá trị của một hoặc nhiều biến độc lập.

Các loại hồi quy

1. Hồi quy tuyến tính cơ bản: Điều này liên quan đến một biến độc lập duy nhất và một biến phụ thuộc. Mối quan hệ giữa hai biến được giả định là tuyến tính, nghĩa là nó có thể được biểu diễn bằng một đường thẳng. Ví dụ: dự đoán giá nhà dựa trên quy mô của ngôi nhà.
2. Hồi quy nhiều tuyến tính: Điều này liên quan đến nhiều hơn một biến độc lập và một biến phụ thuộc. Nó mở rộng hồi quy tuyến tính đơn giản để chứa nhiều yếu tố dự đoán. Ví dụ: dự đoán mức lương của một người dựa trên trình độ học vấn, số năm kinh nghiệm và vị trí của họ.
3. Hồi quy đa thức: Hồi quy đa thức mô hình hóa mối quan hệ giữa biến độc lập và biến phụ thuộc dưới dạng đa thức bậc n. Nó cho phép các mối quan hệ phức tạp hơn giữa các biến mà các mô hình tuyến tính không thể nắm bắt được.
4. Hồi quy logistic: Không giống như hồi quy tuyến tính, hồi quy logistic được sử dụng khi biến phụ thuộc là biến phân loại. Nó dự đoán xác suất xảy ra một sự kiện bằng cách khớp dữ liệu với đường cong logistic. Ví dụ: dự đoán liệu khách hàng có mua sản phẩm hay không dựa trên thông tin nhân khẩu học của họ.

Các bước trong phân tích hồi quy

1. Thu thập dữ liệu: Thu thập dữ liệu về các biến quan tâm.
2. Khám phá dữ liệu: Khám phá dữ liệu để hiểu mối quan hệ giữa các biến, xác định các ngoại lệ và đánh giá chất lượng dữ liệu.
3. Xây dựng mô hình: Chọn mô hình hồi quy phù hợp dựa trên bản chất của dữ liệu và câu hỏi nghiên cứu.
4. Lắp mô hình: Ước tính các tham số của mô hình hồi quy bằng cách sử dụng các kỹ thuật như ước lượng bình phương tối thiểu hoặc ước lượng khả năng tối đa.
5. Đánh giá mô hình: Đánh giá mức độ phù hợp của mô hình và độ chính xác dự đoán của nó bằng cách sử dụng các thước đo như R bình phương, R bình phương được điều chỉnh và sai số bình phương trung bình gốc (RMSE).
6. Diễn dịch: Giải thích các hệ số của mô hình hồi quy để hiểu mối quan hệ giữa các biến và đưa ra dự đoán hoặc rút ra kết luận dựa trên mô hình.

Sự khác biệt chính giữa tương quan và hồi quy

• Mục tiêu:
  • Mối tương quan đo lường cường độ và hướng của mối quan hệ giữa hai biến.
  • Hồi quy mô hình hóa mối quan hệ giữa các biến, cho phép dự đoán và hiểu được những thay đổi trong một biến ảnh hưởng đến biến khác như thế nào.
• Đại diện:
  • Mối tương quan được biểu thị bằng một hệ số duy nhất (ví dụ: Pearson's r), cho biết mức độ liên kết giữa các biến.
  • Hồi quy liên quan đến việc mô hình hóa mối quan hệ giữa các biến thông qua một phương trình, cho phép dự đoán và giải thích tác động của các biến độc lập lên biến phụ thuộc.
• Tính định hướng:
  • Mối tương quan không ngụ ý quan hệ nhân quả và không thiết lập chiều hướng của mối quan hệ giữa các biến.
  • Hồi quy cho phép đánh giá quan hệ nhân quả và hiểu được chiều hướng của mối quan hệ, phân biệt giữa các biến độc lập và biến phụ thuộc.
• Các Ứng Dụng:
  • Phân tích tương quan được sử dụng để hiểu mức độ liên kết giữa các biến và để xác định các mẫu trong dữ liệu.
  • Phân tích hồi quy được sử dụng để dự đoán, giải thích và kiểm tra giả thuyết, cho phép định lượng các mối quan hệ và ước tính các tham số.
• Đầu ra:
  • Tương quan cung cấp một hệ số duy nhất thể hiện cường độ và hướng của mối quan hệ giữa các biến.
  • Hồi quy cung cấp các hệ số (độ dốc và điểm chặn) định lượng mối quan hệ giữa các biến và cho phép dự đoán biến phụ thuộc dựa trên các biến độc lập.

dự án

1. https://psycnet.apa.org/record/1960-06763-000
2. https://link.springer.com/content/pdf/10.3758/BRM.41.4.1149.pdf
3. https://psycnet.apa.org/record/1995-97110-002

Cập nhật lần cuối: ngày 05 tháng 2024 năm XNUMX