Ungleichungen vs. Gleichungen: Differenz und Vergleich

Ungleichheiten stellen die vergleichende Bewertung der Variablen links mit denen rechts des '<'- oder '>'-Zeichens dar. Alternativ stellen Gleichungen die Gleichheit der Variablen auf der linken und rechten Seite des '='-Zeichens dar.

Ungleichungen vergleichen die relative Größe von Werten, während Gleichungen ihre Gleichheit beweisen. Dieser grundlegende Unterschied führt auch zu anderen Unterschieden, die anerkannt werden müssen.

Key Take Away

1. Gleichungen sind mathematische Aussagen, die die Gleichheit zweier Ausdrücke behaupten; Ungleichheiten zeigen eine Beziehung von größer als, kleiner als oder ungleich zwischen zwei Ausdrücken an.
2. Gleichungen können eine endliche Anzahl von Lösungen haben; Ungleichungen können unendlich viele Lösungen haben.
3. Gleichungen stellen einen bestimmten Punkt oder Wert dar; Ungleichungen stellen einen Wertebereich dar, der die Aussage erfüllt.

Ungleichungen vs. Gleichungen

Eine Gleichung ist eine Aussage, die die Gleichheit zwischen zwei Ausdrücken zeigt, um die Werte der Variablen zu ermitteln, die die Gleichung wahr machen. Eine Ungleichung ist eine Aussage, die eine Beziehung zwischen zwei Ausdrücken zeigt, die nicht unbedingt gleich sind, und die zum Vergleich der Werte zweier Variablen verwendet wird.

Vergleichstabelle

Vergleichsparameter	Ungleichheiten	Gleichungen
Definition	Es ist eine mathematische Aussage, die die Ungleichheit und Reihenfolge der Variablen auf der linken und rechten Seite darstellt.	Es handelt sich um eine mathematische Aussage, die die Gleichheit zwischen den Variablen auf der linken und rechten Seite einer Gleichung darstellt.
Verwendete Symbole	Die Zeichen „größer als“ und „kleiner als“ stellen symbolisch die Beziehung zwischen Variablen dar.	Das Gleichheitszeichen wird verwendet, um die Beziehung zwischen Variablen darzustellen. symbolisch
Repräsentationsfunktion	Ungleichheit zwischen den verwendeten Variablen darstellen.	Gleichheit zwischen den verwendeten Variablen darstellen.
Lösungen	Eine Lösungsmenge -mit unendlichen Antworten- ist ein plausibles Ergebnis für eine Ungleichung.	Die Lösung einer Gleichung ist fest und singulär.
Anzahl der Wurzeln	Die Gesamtzahl der Wurzeln für Ungleichungen ist unendlich.	Die Gesamtzahl der Wurzeln für Gleichungen ist eindeutig.

Was sind Ungleichheiten?

Ungleichheiten sind mathematische Aussagen, die die ungleiche Beziehung zwischen einer Reihe von Variablen darstellen. Sie verwenden die Zeichen „>“ oder „<“, um die vergleichende Analyse der verwendeten Variablen anzuzeigen.

Ungleichheiten repräsentieren notwendigerweise die Reihenfolge der Beziehung zwischen den verwendeten Variablen.

Sie werden auch in mathematischen Problemen verwendet, um die relative Größe von Werten zu vergleichen. Ungleichheiten können auf zwei Arten dargestellt werden.

Ihre Darstellung kann einer Gleichung ähneln oder eine einfache Tatsachenfeststellung sein – wie in mathematischen Theoremen. Zum Vergleich werden häufig Ungleichungen verwendet ganze Zahlen, Variablen und andere algebraische Ausdrücke.

Einige Beispiele für Ungleichheiten sind:

'c > d', wobei 'c' größer als 'd' ist.

'c < d', wobei 'c' kleiner als 'd' ist.

Es kann mehrere Varianten zwischen Ungleichungen geben, einschließlich strenger und Verbindung Ungleichheiten. Jede dieser Varianten hat einen vorgegebenen Satz von Regeln, um den resultierenden Lösungssatz zu bestimmen.

Was sind Gleichungen?

Gleichungen sind ebenfalls mathematische Aussagen, die die Gleichheit von Variablen auf der linken und rechten Seite der Aussage darstellen. Sie verwenden das Zeichen „=“, um die Gleichheit der Werte der beiden gegebenen Sätze algebraischer Variablen darzustellen.

In einer Gleichung ist die Lösung immer einheitlich und repräsentativ für die Gleichheit zwischen linker und rechter Seite.

Einige Beispiele für Gleichungen sind:

a + 2 = 30, wobei „a + 2“ und „30“ beides algebraische Ausdrücke sind, getrennt durch das „=“-Zeichen.

5a + 5 = 35, wobei „5a + 5“ und „35“ beides algebraische Ausdrücke sind, getrennt durch das „=“-Zeichen.

Im Allgemeinen enthalten Gleichungen mehr als eine Variable. In den obigen Beispielen bezieht sich das Lösen der Gleichung auf das Ermitteln des Werts der unbekannten Variablen. Gleichungen werden häufig in algebraischen Berechnungen verwendet.

Gleichungen können auch unterschiedlicher Art sein, etwa lineare, simultane und quadratische Gleichungen.

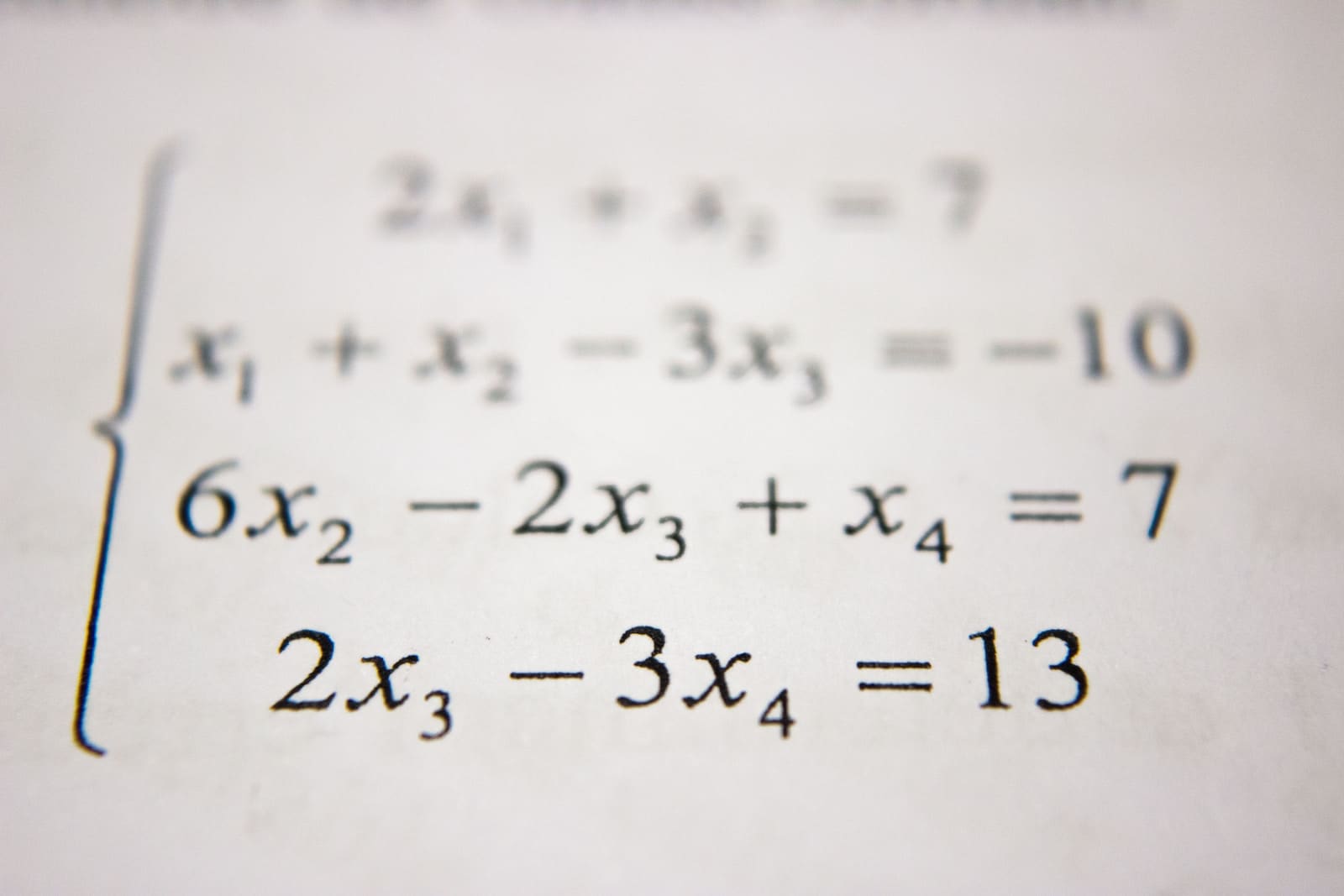
Hauptunterschiede zwischen Ungleichungen und Gleichungen

1. Der Hauptunterschied zwischen Ungleichungen und Gleichungen besteht in ihren Definitionen, die ihre Funktionalitäten in mathematischen Operationen beschreiben. Wie der Name schon sagt, stellt eine Gleichung die Gleichheit zwischen zwei Variablen in der gegebenen Formulierung dar.
   Die linke Seite einer Gleichung ist immer gleich der rechten Seite. Ungleichungen hingegen sind mathematische Aussagen über die Ungleichheit zwischen Variablen. Die linke und rechte Seite von Ungleichheiten stellen Variablen als größer oder kleiner als dar, was ihre Ungleichheit und relative Größe hervorhebt.
2. Der zweite grundlegende Unterschied zwischen den beiden besteht darin, was sie jeweils repräsentieren. Während Ungleichungen die Ungleichheit zwischen zwei Variablen bedeuten, stellen Gleichungen die Gleichheit zwischen zwei variablen Größen dar.
3. Die Symbole, die verwendet werden, um Gleichheit und Ungleichheit in jedem von ihnen auszudrücken, sind ebenfalls unterschiedlich. Ungleichungen verwenden die Symbole „>“ und „<“, um die Ungleichheit zwischen Variablen darzustellen, während Gleichungen die Gleichheit zwischen gegebenen Variablen darstellen, indem sie alphabetische Symbole wie „a“ und „b“ verwenden, begleitet von dem obligatorischen „Gleichheitszeichen“ zwischen links und rechts Seiten.
   Im ersten Fall werden Ungleichheitszeichen verwendet, im zweiten Fall werden Gleichheitszeichen implementiert.
4. Ungleichungen und Gleichungen unterscheiden sich auch deutlich hinsichtlich ihrer möglichen Lösungen. Bei Ungleichheiten können Mehrfachnennungen möglich sein. Als passende Lösung für Ungleichungen wird eine „Lösungsmenge“ vorgegeben, die aus unendlich vielen Werten besteht. Andererseits kann für eine Gleichung nur eine Antwort ermittelt werden.
5. Schließlich ist die Gesamtzahl der Wurzeln einer Gleichung eindeutig. Dies gilt nicht für Ungleichheiten.

\

Bibliographie

1. https://ieeexplore.ieee.org/abstract/document/754846/
2. http://www.mathematik.uni-dortmund.de/~erme/CERME4/CERME4_WG6.pdf#page=24

Letzte Aktualisierung: 11. Juni 2023