Cos'è il test T? | Definizione, Calcolo, Formula vs Esempi

Un test T è uno strumento statistico utilizzato per il test di ipotesi per confrontare la media di due insiemi di dati osservati e determinare il loro tasso di differenza.

Rientra nell'ambito della statistica inferenziale, il ramo che si occupa di fare previsioni e generalizzazioni su una data popolazione prelevando un campione.

A differenza di Test Z, la dimensione del campione in un test T dovrebbe essere inferiore a 30 e la deviazione standard dovrebbe essere sconosciuta.

Punti chiave

1. Il test T è un test statistico utilizzato per determinare se le medie di due gruppi di dati sono significativamente diverse l'una dall'altra.
2. Il test T è comunemente utilizzato nella ricerca scientifica per analizzare i risultati di esperimenti o sondaggi e per trarre conclusioni sulla popolazione da cui è stato tratto il campione.
3. Il test T può essere utilizzato per testare ipotesi, confrontare l'efficacia di diversi trattamenti o esaminare la relazione tra due variabili.

Origine del test T

A Prova T è stato condotto per la prima volta da William Sealy Gosset, uno statistico, chimico e birraio inglese. Mentre lavorava per un'azienda produttrice di birra chiamata Guinness, ha applicato il t-test per osservare il carattere coerente della birra scura.

Alla fine, questo test è stato aggiornato con la sua connotazione attuale, riferendosi a qualsiasi test di ipotesi le cui variabili di dati seguono una distribuzione t (una curva a campana con code pesanti) se l'ipotesi nulla si dimostra accurata.

Quando è possibile eseguire un test T?

Un test T deve rispettare le seguenti condizioni per un'interpretazione e una convalida standard.

1. Gli insiemi di dati osservati non dovrebbero essere più di due.
2. I dati devono essere campionati in modo casuale.
3. La dimensione del campione non deve essere superiore a 30.
4. Le variabili dei dati devono essere indipendenti.
5. Le variabili dei dati devono riflettere una distribuzione approssimativamente normale.
6. La varianza deve essere sconosciuta e omogenea.
7. L'esito della scala di misura applicata ai dati raccolti deve seguire una linea continua.

Quale tipo di test T è più adatto?

La scelta di un tipo di test T dipenderà principalmente da due cose:

1. Se i set di dati raccolti appartengono alla stessa o a due popolazioni diverse.
2. Il conduttore di prova intende esaminare la differenza in una particolare direzione.

Basato sul natura della popolazione campione, un test T può essere classificato in tre tipi.

1. Un campione T-test: Implica il confronto della media di un singolo set di dati con una media nota o un valore standard.
2. Test T campioni accoppiati: Implica il confronto della media di un singolo insieme di dati osservati a intervalli diversi prima e dopo un esperimento.
3. Test T campioni indipendenti: Conosciuto anche come Test T a due campioni, comporta il confronto di due diversi insiemi di dati osservati e le loro medie.

Basato sul del conduttore di prova intenzione di esaminare la differenza in una particolare direzione, un test T può essere classificato nei seguenti due tipi.

1. Determina il test T a una coda se la media di una popolazione è minore o maggiore dell'altra media della popolazione.
2. Test T a due code: Viene utilizzato per determinare se esiste una differenza tra due set di dati.

Come condurre un test T?

Un test T misura la reale differenza tra le medie di due gruppi campione utilizzando il rapporto tra la differenza nelle medie del gruppo campione e l'errore standard aggregato di entrambi i gruppi campione.

La seguente formula può essere utilizzata per eseguire un test t a due campioni o di Student:

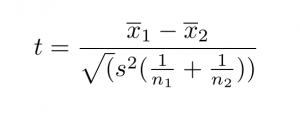
Qui,

• t = valore del test T
• x1 _ed x2 = Medie dei due gruppi campione
• s2= Errore standard raggruppato dei due gruppi campione
• n1 e n2 = Numero di osservazioni in ciascun gruppo campione

Per determinare se il valore t calcolato è superiore al valore t previsto per caso, è necessario utilizzare un grafico del valore critico e confrontare il valore t calcolato con il valore t critico.

Se il valore t calcolato è effettivamente più alto, implica che l'ipotesi nulla viene respinta. Di conseguenza, si può concludere che i gruppi campione sono effettivamente diversi.

Cos'è il punteggio t?

Un t-score o t-value è un numero che rappresenta l'entità della differenza tra le medie di due insiemi di dati osservati.

Un t-score più alto implica che i gruppi campione sono diversi. Al contrario, un punteggio t più piccolo indica somiglianze tra i gruppi campione.

Vantaggi del test T

Di seguito sono riportati alcuni notevoli vantaggi del test T:

1. È uno dei strumenti più semplici e versatili per confrontare due insiemi di dati.
2. L'output delle variabili indipendenti è facile da interpretare.
3. Richiede una piccola dimensione del campione. Di conseguenza, la raccolta dei dati è relativamente più comoda sotto un t-test.
4. Viene utilizzato per determinare se due insiemi di dati campione appartengono alla stessa popolazione. Di conseguenza, aiuta a entrare ottenere la fonte dei dati.

Svantaggi del test T

Come strumento per la verifica delle ipotesi, il test T è piuttosto conservativo. Di seguito sono riportate alcune limitazioni significative del test T.

1. Solo è possibile confrontare due insiemi di dati campione utilizzando un test T.
2. L'assunzione di i dati del campione essendo casuali non sono sempre corretti.
3. Anche se un test T può aiutare a determinare l'origine di un determinato set di dati, i fattori ambientali possono influenzare significativamente i suoi risultati e rendere i risultati inaffidabili.

Riferimenti

1. https://www.ncbi.nlm.nih.gov/pmc/articles/pmc4667138/
2. https://scholarworks.umass.edu/cgi/viewcontent.cgi?article=1307&context=pare
3. https://onlinelibrary.wiley.com/doi/abs/10.1002/bimj.4710280202

Ultimo aggiornamento: 11 giugno 2023