微分と統合: 違いと比較

微積分は当初、微積分または「微積分の微積分」として知られていました。 微積分は 17 世紀に登場しました。

小石を使って何かを計算するようなものなのでそう呼ばれています。 微積分の微分は、何かを小さなビットに分割して、その変化を知ることです。 微積分の積分では、小さなビットを結合して量を知ることができます。

歯石 継続的な変化の研究です。

2 主要な 微積分で使用されるブランチは、微分と積分です。 その他にもたくさんのグーグルの 学生や学者でさえ、その違いを理解することができません。

主要な取り組み

1. 微分は、特定の点での関数の変化率または勾配を計算する微積分の数学演算です。
2. 積分は微分の逆演算であり、特定の間隔にわたる関数の値の累積合計を計算し、面積、体積、またはその他の量を求めるために使用されます。
3. 微積分と積分はどちらも微積分の重要な概念ですが、変化率に焦点を当てた微分と累積に焦点を当てた積分という反対の目的を果たします。

差別化と統合

微分と積分の違いは、微分を使用して瞬時の変化率と曲線の傾きを見つけることです。 もし、あんたが する必要が 曲線下の面積を計算するには、積分を使用します。 ご覧のとおり、微分と積分は数学的な意味で互いに反対です。

---

 

比較表

比較のパラメータ	分化	統合
目的	微分は、曲線の勾配を計算するために使用されます。 あるポイントから別のポイントへの瞬間的な変化率を見つけるために使用されます。	積分は、曲線の下または曲線間の面積を計算するために使用されます。
実際のアプリケーション	瞬時速度の計算には微分が使用されます。 また、関数が増加しているか減少しているかを調べるためにも使用されます。	積分は、曲面の面積を計算するために使用されます。 また、オブジェクトの体積を計算するためにも使用されます。
足し算と割り算	微分は、除算を使用して、瞬間速度または目的の結果を計算します。	積分は計算に足し算を使用します。
真向かい	微分は、統合の逆のプロセスです。	統合は分化の逆のプロセスです。
職種	関数の速度を計算するために微分が使用され、瞬間速度が計算されます。	積分は、曲線の下の面積を計算するときに、関数がカバーする距離を計算するために使用されます。

---

 

差別化とは？

数学で、関数の変化率または デリバティブ 微分として知られています。

XNUMX つの派生物は次のとおりです。

1. 代数関数- D(xⁿ）= nx^{n - 1} 
2. 三角関数- D（それなし x）= cos x
3. 指数関数- D(e^x）= e^x

微分は、曲線の勾配を計算し、ある点から別の点への瞬間的な変化率を見つけるために使用されます。

複合関数を区別するのに役立つ「連鎖規則」があります。 瞬時速度の計算は、微分のリアルタイム使用の XNUMX つです。

 

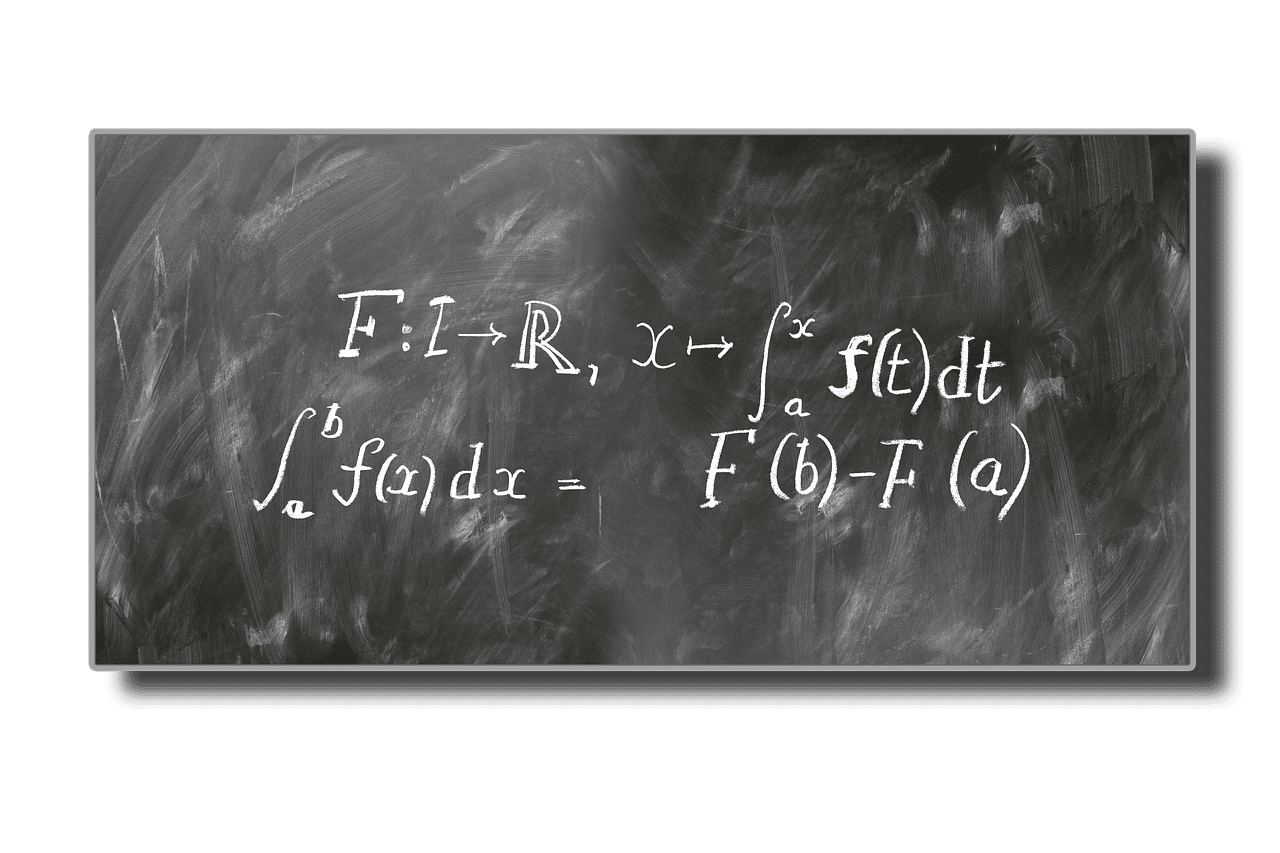
統合とは

微積分では、積分は、曲線の下の面積を計算するために使用される式と方法を指します。 サイトを計算できる完全な形状ではないため、そのように計算するために使用されます。

積分は、任意の関数によって移動した距離を見つけるために使用されます。 関数が移動した距離は、曲線の下の領域です。

最終更新日 : 11 年 2023 月 XNUMX 日