Что такое Т-тест? | Определение, расчет, формула и примеры

Т-тест — это статистический инструмент, используемый для проверки гипотез для сравнения среднего значения двух наборов наблюдаемых данных и определения степени их различия.

Это относится к области статистики вывода, области, связанной с предсказаниями и обобщениями в отношении данной совокупности путем отбора выборки.

В отличие от в Z-тест, размер выборки в Т-критерии должен быть меньше 30, а стандартное отклонение должно быть неизвестно.

Основные выводы

1. Т-тест — это статистический тест, используемый для определения того, значительно ли отличаются друг от друга средние значения двух групп данных.
2. Т-критерий обычно используется в научных исследованиях для анализа результатов экспериментов или опросов и для получения выводов о населении, из которого была взята выборка.
3. Т-тест можно использовать для проверки гипотез, сравнения эффективности различных методов лечения или изучения взаимосвязи между двумя переменными.

Происхождение Т-теста

A Т-тест был впервые проведен Уильямом Сили Госсетом, английским статистиком, химиком и пивоваром. Работая в пивоваренной компании Guinness, он применил t-критерий, чтобы наблюдать за неизменным характером стаута.

В конце концов, этот тест был обновлен с его нынешним значением, относящимся к любому тесту гипотезы, переменные данных которого следуют t-распределению (колоколообразная кривая с весомыми хвостами), если нулевая гипотеза оказывается точной.

Когда можно проводить Т-тест?

T-тест должен соответствовать следующим условиям для стандартной интерпретации и проверки.

1. Наборов наблюдаемых данных не должно быть более двух.
2. Данные должны выбираться случайным образом.
3. Объем выборки не должен превышать 30.
4. Переменные данных должны быть независимыми.
5. Переменные данных должны отражать приблизительно нормальное распределение.
6. Дисперсия должна быть неизвестной и однородной.
7. Результат шкалы измерения, применяемой к собранным данным, должен следовать непрерывной линии.

Какой вид Т-теста наиболее подходит?

Выбор типа Т-теста в первую очередь будет зависеть от двух вещей:

1. Принадлежат ли собранные наборы данных одной или двум разным группам населения.
2. Проводник-испытатель намеревается исследовать разницу в определенном направлении.

На основе характер выборочной совокупности, Т-тест можно разделить на три типа.

1. Один образец Т-теста: Это влечет за собой сравнение среднего значения одного набора данных с известным средним или стандартным значением.
2. Парный образец Т-теста: Он включает в себя сравнение среднего значения одного набора наблюдаемых данных через разные промежутки времени до и после эксперимента.
3. Т-тест независимых выборок: Также известный под названием Двухвыборочный Т-тест, это влечет за собой сравнение двух разных наборов наблюдаемых данных и их средних значений.

На основе проводник-испытатель намерение исследовать разницу в определенном направлении, Т-тест можно разделить на следующие два типа.

1. Односторонний Т-критерий определяет является ли среднее значение населения меньше или больше, чем другое среднее значение населения.
2. Двусторонний Т-тест: Он используется, чтобы определить, есть ли разница между двумя наборами данных.

Как провести Т-тест?

T-тест измеряет реальную разницу между средними значениями двух выборочных групп, используя отношение разности средних значений группы выборки к объединенной стандартной ошибке обеих групп выборки.

Следующая формула может использоваться для запуска двухвыборочного или t-критерия Стьюдента:

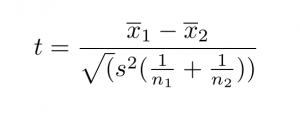
Здесь,

• t = значение Т-теста
• x1 _и х2 = Средние значения двух выборочных групп
• с2 = Объединенная стандартная ошибка двух групп образцов
• п1 и п2 = Количество наблюдений в каждой выборочной группе

Чтобы определить, превышает ли вычисленное значение t случайно ожидаемое значение t, необходимо использовать диаграмму критических значений и сравнить вычисленное значение t с критическим значением t.

Если вычисленное значение t действительно выше, это означает, что нулевая гипотеза отвергнута. Соответственно, можно сделать вывод, что выборочные группы действительно разные.

Что такое t-показатель?

Т-оценка или t-значение — это число, которое представляет степень различия между средними значениями двух наборов наблюдаемых данных.

Более высокий t-показатель означает, что группы выборки различны. Напротив, меньший t-показатель означает сходство между группами выборки.

Преимущества Т-теста

Ниже приведены некоторые заметные преимущества Т-теста:

1. Это один из самые простые и универсальные инструменты для сравнения двух наборов данных.
2. Выход независимых переменных легко интерпретировать.
3. Для этого требуется небольшой размер выборки. Следовательно, сбор данных относительно более удобен по t-критерию.
4. Он используется для определения того, принадлежат ли два набора выборочных данных одной и той же генеральной совокупности. Следовательно, помогает в получение источника данных.

Недостатки Т-теста

Как инструмент проверки гипотез, Т-тест довольно консервативен. Ниже приведены некоторые существенные ограничения T-теста.

1. Только можно сравнить два набора выборочных данных с помощью Т-теста.
2. Предположение о выборочные данные, являющиеся случайными, не всегда верны.
3. Несмотря на то, что Т-тест может помочь определить источник данного набора данных, факторы окружающей среды могут существенно повлиять на его результаты и сделать результаты ненадежными.

Рекомендации

1. https://www.ncbi.nlm.nih.gov/pmc/articles/pmc4667138/
2. https://scholarworks.umass.edu/cgi/viewcontent.cgi?article=1307&context=pare
3. https://onlinelibrary.wiley.com/doi/abs/10.1002/bimj.4710280202

Последнее обновление: 11 июня 2023 г.