- Enter the force (F) and spring constant (k) along with their respective units.
- Enter the displacement (x) along with its unit.
- Click "Calculate" to calculate Hooke's Law.
- View the result, detailed calculation, and the Force-Displacement chart.
- Your calculation history is displayed below the calculator.
- Click "Copy Result" to copy the result to the clipboard.
- Use "Clear" to reset the calculator and start a new calculation.
Hooke’s Law Calculator is a tool designed to simplify the process of calculating the force in a spring or elastic material, based on its extension or compression. This calculator is rooted in Hooke’s Law, a principle fundamental to physics and engineering, especially within the fields of mechanics and material science.
Understanding Hooke’s Law
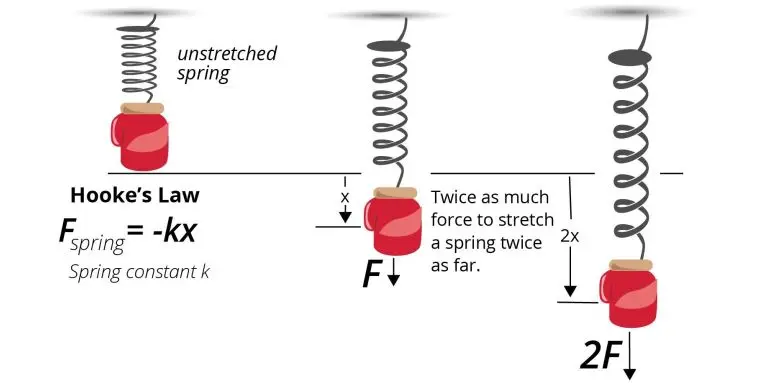
Concept of Hooke’s Law
Hooke’s Law states that the force needed to extend or compress a spring by some distance is proportional to that distance. This principle can be mathematically expressed as:
F = -k * x
Where:
Fis the force applied to the spring (in Newtons, N)kis the spring constant (in Newtons per meter, N/m)xis the displacement of the spring from its equilibrium position (in meters, m)- The negative sign indicates that the force is in the opposite direction of the displacement.
Spring Constant (k)
The spring constant k is a measure of the stiffness of the spring. A higher k value means the spring is stiffer, and more force is required to extend or compress it by a certain amount.
Formulae Related to Hooke’s Law
Potential Energy in a Spring
The potential energy stored in a compressed or extended spring can be calculated using the formula:
PE = 1/2 * k * x^2
Where PE is the potential energy (in Joules, J).
Oscillations and Hooke’s Law
Hooke’s Law also plays a crucial role in harmonic oscillation, where the period T (time for one complete cycle) of a mass m attached to a spring is given by:
T = 2 * π * sqrt(m/k)
Benefits of Using Hooke’s Law Calculator
Accuracy and Efficiency
The calculator eliminates human errors in calculation, ensuring accurate and swift results. This is particularly beneficial in engineering and physics where precision is paramount.
User-Friendly
It’s designed to be intuitive, requiring users to input only the basic parameters (displacement, spring constant) to get the force or potential energy, making complex calculations accessible even to those with limited physics background.
Versatility
The calculator can be used in various scenarios, from academic problems to real-life applications like engineering design and material testing.
Interesting Facts about Hooke’s Law
Historical Context
Hooke’s Law is named after the 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram, and then published the solution in 1678 as “ut tensio, sic vis” meaning “as the extension, so the force.”
Beyond Springs
Although most commonly associated with springs, Hooke’s Law is also applicable to other situations where an elastic body is deformed, like the stretching of a rubber band or the bending of a beam.
Limitations – The Elastic Limit
Hooke’s Law is only valid up to the elastic limit of the material. Beyond this point, the material may deform permanently or break, and the law no longer applies. This threshold is crucial in material science and engineering.
Conclusion
Hooke’s Law Calculator is more than just a computational tool; it embodies a fundamental principle of physics that describes the elasticity of materials. Its applications range from academic exercises to complex engineering designs, making it an indispensable tool in science and technology. The simplicity of Hooke’s Law belies the complexity of the natural world it helps to describe, and the calculator serves as a bridge between theoretical physics and practical application.
For a comprehensive understanding and further reading, the following references provide detailed insights into Hooke’s Law and its applications:
- “Physics for Scientists and Engineers” by Raymond A. Serway and John W. Jewett – A textbook offering a detailed explanation of Hooke’s Law in the context of classical mechanics.
- “Materials Science and Engineering: An Introduction” by William D. Callister Jr. and David G. Rethwisch – This book discusses the microscopic interpretation of Hooke’s Law and its relevance in material science.
- “Mechanical Behavior of Materials” by Thomas H. Courtney – This resource delves into the implications of Hooke’s Law in the field of material testing and structural analysis.
Last Updated : 12 February, 2024
I’ve put so much effort writing this blog post to provide value to you. It’ll be very helpful for me, if you consider sharing it on social media or with your friends/family. SHARING IS ♥️
Emma Smith holds an MA degree in English from Irvine Valley College. She has been a Journalist since 2002, writing articles on the English language, Sports, and Law. Read more about me on her bio page.
