Calculus was initially known as infinitesimal calculus or “the calculus of infinitesimals”. Infinitesimals calculus came about in the 17th century.
It is called so because it is like using small pebbles for calculating something. Differentiation in calculus cuts something into small bits to know about its changes. Integration in Calculus joins the small bits together to know the quantities.
Calculus is the study of continuous change.
The two major branches used in calculus are Differentiation and Integration. Many students and even scholars are not able to understand its difference.
Key Takeaways
- Differentiation is a mathematical operation in calculus that calculates a function’s rate of change or slope at a specific point.
- Integration is the inverse operation of differentiation, computing the accumulated sum of a function’s values over a given interval, used to find areas, volumes, or other quantities.
- Both differentiation and integration are essential concepts in calculus, but they serve opposite purposes, with differentiation focusing on rates of change and integration on accumulation.
Differentiation vs Integration
The difference between Differentiation and Integration is that differentiation is used to find the instant rates of change and the slopes of curves. If you need to calculate the area under curves, use Integration. As you can see, both differentiation and integration are opposite to each other in mathematical significance.
Comparison Table
| Parameters of Comparison | Differentiation | Integration |
|---|---|---|
| Purpose | Differentiation is used to calculate the gradient of a curve. It is used to find out the instant rates of change from one point to another. | Integration is used to calculate the area under or between the curves. |
| Real-life application | Differentiation is used to calculate instant velocity. It is also used to find whether a function is increasing or decreasing. | Integration is used to calculate the area of curved surfaces. It is also used to calculate the volume of objects. |
| Addition and division | Differentiation uses division to calculate the instant velocity or any desired results. | The integration uses addition for its calculations. |
| Directly opposite | Differentiation is the reversed process of integration. | Integration is the reversed process of differentiation. |
| Role | Differentiation is used to calculate the speed of the function as it calculates instant velocity. | Integration is used to calculate the distance covered by any function as it calculates the area under the curve. |
What is Differentiation?
In mathematics, the method of finding the rate of change of a function or finding the derivative is known as Differentiation.
The three derivatives are:
- Algebraic functions- D(xn) = nxn − 1
- Trigonometric functions- D(sin x) = cos x
- Exponential functions- D(ex) = ex
Differentiation is used to calculate the gradient of a curve and to find out the instant rates of change from one point to another.
There is a ‘chain rule’ which helps to differentiate composite functions. Calculation of instant velocity is one of the real-time use of differentiation.
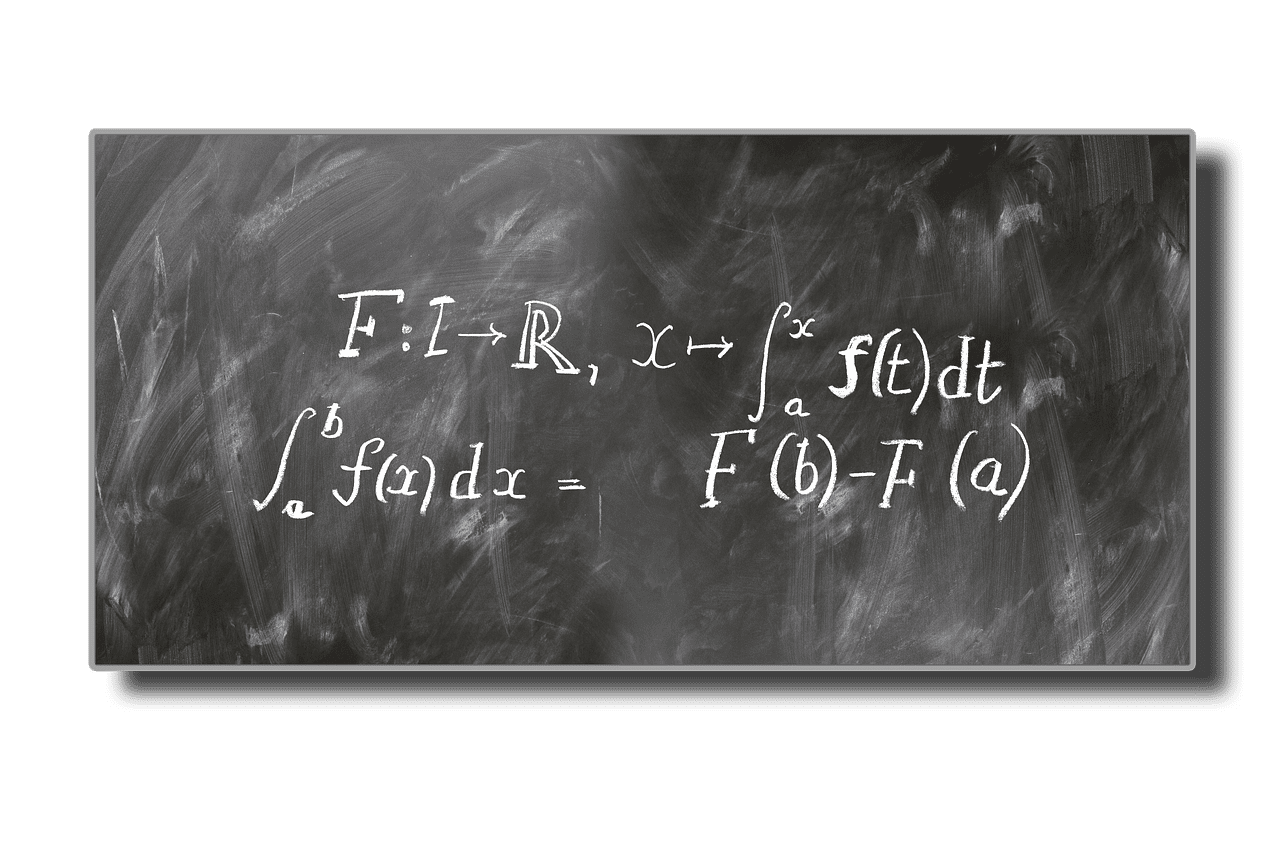
What is Integration?
In calculus, integration refers to the formula and the method used to calculate the area under the curve. It is used to calculate so because it is not a perfect shape for which the site can be calculated.
Integration is used to find the distance moved by any function. The distance travelled by the function is the area under the curve.
I’ve put so much effort writing this blog post to provide value to you. It’ll be very helpful for me, if you consider sharing it on social media or with your friends/family. SHARING IS ♥️
The practical implications of Integration and its role in calculating real-world values are explained effectively. It bridges the gap between theory and application.
Indeed, understanding the role of Integration in practical scenarios can enhance one’s appreciation for its significance.
This is an article for beginners who want to understand the basics of calculus. The explanation of Differentiation and Integration is well articulated.
I agree, the article serves as a useful resource for those who want to build a strong foundation in calculus.
The distinction between algebraic, trigonometric, and exponential functions in Differentiation is well elucidated, contributing to a deeper understanding of derivatives.
Absolutely, the breakdown of derivative types provides a comprehensive overview of Differentiation.
The section on ‘What is Differentiation?’ gives a clear understanding of the purpose and use of Differentiation, making it easier for individuals to comprehend.
Definitely, highlighting the real-time use of Differentiation provides valuable context for its application.
The ‘chain rule’ explanation was particularly insightful. It adds depth to the discussion of Differentiation.
The historical context provided about calculus is enlightening. It’s crucial to understand the origins of such a pivotal mathematical discipline.
I found the explanation about Differentiation vs Integration very clear and informative. It helped me grasp the concept better.
Definitely, the breakdown of their differences can aid in solidifying one’s understanding of calculus.
The article presents a comprehensive overview of Differentiation and Integration. Its emphasis on real-life applications makes it more engaging.
I couldn’t agree more. Relating calculus to real-world examples aids in capturing the interest of learners.
The concept of Differentiation and Integration can be seen in various real-life applications. Understanding this can provide valuable insights in many fields.
Absolutely, the applicability of calculus extends beyond the academic realm and can be beneficial in practical scenarios.
Indeed, grasping calculus concepts can unlock numerous opportunities in diverse industries.
The explanation of Integration as a method for calculating the area under the curve is articulated in a manner that simplifies this complex concept.
Agreed, the clarity of explanation renders Integration more accessible to a wide audience.
The comparison table provided is a handy reference for understanding the nuances of Differentiation and Integration. It simplifies complex concepts.