A conic section is a curve obtained when a plane intersects a cone at some specific angle. There are three conic sections – ellipse, parabola, and hyperbola.
An ellipse is a planar curve with two focal points that resemble a circle. However, the parabola and hyperbola are confusing sections.
Key Takeaways
- Parabolas are U-shaped curves representing quadratic functions, with one axis of symmetry and a single vertex.
- Hyperbolas consists of two distinct curves, representing points with a constant difference between distances between two foci.
- Both parabolas and hyperbolas are conic sections, but they exhibit different shapes and mathematical properties, with parabolas having a single branch and hyperbolas having two branches.
Parabola vs Hyperbola
Parabola is a U-shaped curve that is symmetrical around its axis. In contrast, a hyperbola is a type of curve that has two branches that open up or down and are symmetrical around their centre point. In math, they are represented by different equations and have different properties.
A parabola is a single open curve that extends to infinity. It is U-shaped and has one focus and one directrix.
A hyperbola is an open curve having two unconnected branches. It has two foci and two directrices, one for each unit.
Comparison Table
| Parameter Of Comparison | Parabola | Hyperbola |
|---|---|---|
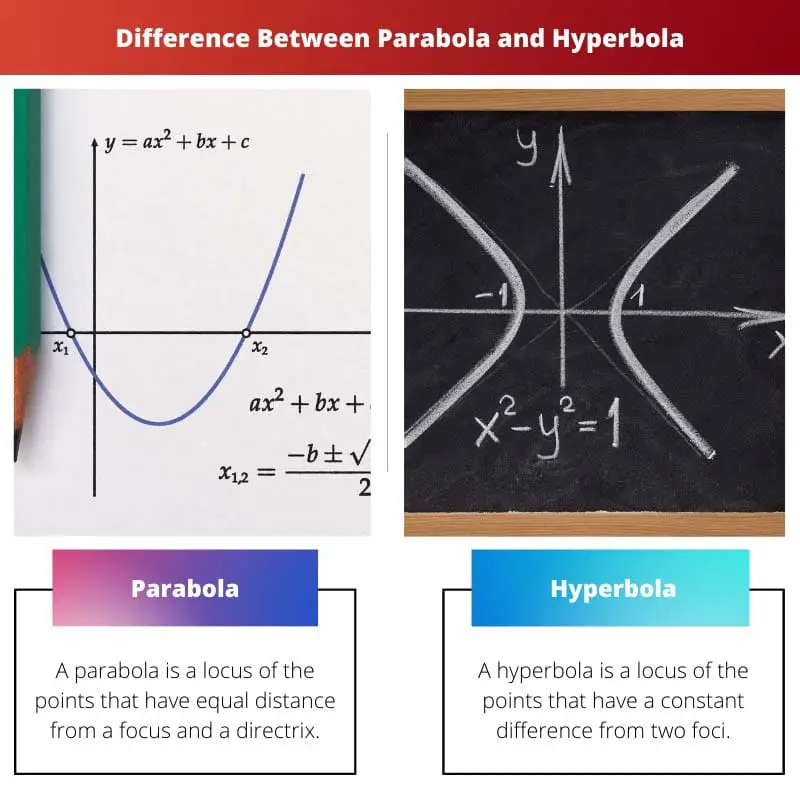
| Definition | A parabola is a locus of the points with an equal distance from a focus and a directrix. | A hyperbola is a locus of the points with a constant difference between two foci. |
| Shape | The parabola is an open curve that has one focus and one directrix. | The hyperbola is an open curve with two branches, two foci, and two directrices. |
| Eccentricity | The non-negative eccentricity of a parabola is one. | The non-negative eccentricity e of a hyperbola is more significant than one. |
| Intersection of Plane | The intersection of the plane is parallel (ideal case) to the slant height of the cone. | The intersection of the plane is parallel (ideal case) to the perpendicular height of the double cone. |
| General Equation | The general equation of the parabola is y = ax², a ≠ 0 | The general equation of the hyperbola is x²/a² – y²/b² = 1 |
What is Parabola?
A parabola is the locus of all the points equidistant from a point and a line. This point is called the focus, and this line is called the directrix.
A parabola is formed when a plane intersects a cone in a parallel direction (ideal case) to its slant height.
The general equation of a parabola is given as
y = ax², a ≠ 0
The value of a determines the shape of the curve.
If a > 0, the mouth of the parabola opens to the top.
If a < 0, the mouth of the parabola opens to the bottom.
The focus of the above parabola is (0, 1/4a). The directrix is (-1/4a).
However, when a=1, the parabola is called a unit parabola.
A parabola has an eccentricity of one.
A parabola is symmetric about its axis. At an infinite distance, the curves appear as parallel lines.
What is Hyperbola?
A hyperbola is the locus of all the points with a constant difference between two distinct points. These points are called the foci of the hyperbola.
A hyperbola is formed when a solid plane intersects a cone in a direction parallel to its perpendicular height.
The general equation of a hyperbola is given as
(x-α) ²/a² – (y-β)²/b² = 1
The foci of the above hyperbola are ( α ± sqrt( a²+b²), β).
The vertices are (±a, β).
A hyperbola has an eccentricity more significant than one.
A hyperbola has two axes of symmetry. These are the transverse axis and the conjugate axis.
Main Differences Between Parabola and Hyperbola
A parabola and a hyperbola are conic sections. They have different shapes and properties.
The main differences between the two are :
- A parabola is a locus of all the points with an equal distance from a focus and a directrix. On the other hand, a hyperbola is a locus of all the issues for which the difference in distance between two foci is constant.
- A parabola is an open curve with one focus and directrix, whereas a hyperbola is an open curve with two branches with two foci and directrices.
- The eccentricity of a parabola is one, whereas the eccentricity of a hyperbola is more significant than one.
- A parabola is formed when the plane intersects a cone along its slant height. On the other hand, a hyperbola is formed when the plane intersects a cone along its perpendicular height.
- The equation for a parabola is y = ax². On the other hand, the equation for a hyperbola is x²/a² – y²/b² = 1.
- https://www.osapublishing.org/abstract.cfm?uri=ao-54-24-7148
- https://asmedigitalcollection.asme.org/appliedmechanics/article-abstract/68/4/537/449711
I’ve put so much effort writing this blog post to provide value to you. It’ll be very helpful for me, if you consider sharing it on social media or with your friends/family. SHARING IS ♥️
Great article! I appreciate the clear and concise explanation of the differences between parabolas and hyperbolas. This was very informative.
I agree, Tanya. The distinction between parabolas and hyperbolas is very well-explained here.
The tone of the article is very academic, making it hard to understand for those who aren’t mathematically inclined.
That’s a good point, Rhall. A more accessible tone could be beneficial.
This article is a great resource for anyone studying conic sections. It’s very well-written and informative.
I agree, it’s a valuable resource for students looking to understand this topic.
The presentation of concepts is very clear and informative. I appreciate the emphasis on key differences.
The emphasis on the contrast is very helpful in understanding the concepts.
I concur, Ross. The presentation is excellent, highlighting the key distinctions between parabolas and hyperbolas.
The explanation of conic sections is clear and concise. I would’ve liked to see more detailed examples, though.
I agree, Xrussell. More examples would have been beneficial.
I fail to see the relevance of this article. I feel like this is information most people were already familiar with. It’s a bit redundant.
I think the article provides a detailed comparison, even for those well-versed in mathematics.
This article provides a great comparison between parabolas and hyperbolas. It is very well-researched and detailed.
Absolutely, Owen. The depth of information is commendable.
I echo your sentiments, Owen. The research is evident in this article.
I find the article to be a bit too technical. It could benefit from a more layman’s explanation of the concepts.
Agreed. A simplified version could make the content more accessible.
I see your point, Matilda. A simplified version would be helpful for a wider audience.
I am glad that the article includes comparison tables. It really helps in understanding the differences.
I agree, Ruby. The tables are a very useful addition to the article.
Absolutely, Ruby. The visual representation is beneficial in this context.
I find the comparison in this article to be oversimplified. There is more depth to these topics than what’s presented here.
I see your point, Graham. A more in-depth analysis could enhance this article.